Time-Domain Based Modeling :: Special Topics (Signal Processing Toolbox)

Signal Processing Toolbox

Time-Domain Based Modeling

The lpc, prony, and stmcb functions find the coefficients of a digital rational transfer function that approximates a given time-domain impulse response. The algorithms differ in complexity and accuracy of the resulting model.

Linear Prediction

Linear prediction modeling assumes that each output sample of a signal, x(k), is a linear combination of the past n outputs (that is, it can be "linearly predicted" from these outputs), and that the coefficients are constant from sample to sample:

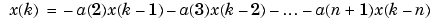
An nth-order all-pole model of a signal x is

```
a = lpc(x,n)
```

To illustrate lpc, create a sample signal that is the impulse response of an all-pole filter with additive white noise:

randn('state',0);
x = impz(1,[1 0.1 0.1 0.1 0.1],10) + randn(10,1)/10;

The coefficients for a fourth-order all-pole filter that models the system are

a = lpc(x,4)
a = 
    1.0000    0.2574    0.1666    0.1203    0.2598

lpc first calls xcorr to find a biased estimate of the correlation function of x, and then uses the Levinson-Durbin recursion, implemented in the levinson function, to find the model coefficients a. The Levinson-Durbin recursion is a fast algorithm for solving a system of symmetric Toeplitz linear equations. lpc's entire algorithm for n = 4 is

r = xcorr(x);
r(1:length(x)-1) = [];       % Remove corr. at negative lags
a = levinson(r,4)
a =
    1.0000    0.2574    0.1666    0.1203    0.2598

You could form the linear prediction coefficients with other assumptions by passing a different correlation estimate to levinson, such as the biased correlation estimate:

r = xcorr(x,'biased');
r(1:length(x)-1) = [];       % Remove corr. at negative lags
a = levinson(r,4)
a =
    1.0000    0.2574    0.1666    0.1203    0.2598

Prony's Method (ARMA Modeling)

The prony function models a signal using a specified number of poles and zeros. Given a sequence x and numerator and denominator orders n and m, respectively, the statement

```
[b,a] = prony(x,n,m)
```

finds the numerator and denominator coefficients of an IIR filter whose impulse response approximates the sequence x.

The prony function implements the method described in [4] Parks and Burrus (pgs. 226-228). This method uses a variation of the covariance method of AR modeling to find the denominator coefficients a, and then finds the numerator coefficients b for which the resulting filter's impulse response matches exactly the first n + 1 samples of x. The filter is not necessarily stable, but it can potentially recover the coefficients exactly if the data sequence is truly an autoregressive moving-average (ARMA) process of the correct order.

Note The functions prony and stmcb (described next) are more accurately described as ARX models in system identification terminology. ARMA modeling assumes noise only at the inputs, while ARX assumes an external input. prony and stmcb know the input signal: it is an impulse for prony and is arbitrary for stmcb.

A model for the test sequence x (from the earlier lpc example) using a third-order IIR filter is

[b,a] = prony(x,3,3)
b =
    0.9567   -0.3351    0.1866   -0.3782
a =
    1.0000   -0.0716    0.2560   -0.2752

The impz command shows how well this filter's impulse response matches the original sequence:

format long
[x impz(b,a,10)]
ans =
   0.95674351884718   0.95674351884718
  -0.26655843782381  -0.26655843782381
  -0.07746676935252  -0.07746676935252
  -0.05223235796415  -0.05223235796415
  -0.18754713506815  -0.05726777015121
   0.15348154656430  -0.01204969926150
   0.13986742016521  -0.00057632797226
   0.00609257234067  -0.01271681570687
   0.03349954614087  -0.00407967053863
   0.01086719328209   0.00280486049427

Notice that the first four samples match exactly. For an example of exact recovery, recover the coefficients of a Butterworth filter from its impulse response:

[b,a] = butter(4,.2);
h = impz(b,a,26);
[bb,aa] = prony(h,4,4);

Try this example; you'll see that bb and aa match the original filter coefficients to within a tolerance of 10^-13.

Steiglitz-McBride Method (ARMA Modeling)

The stmcb function determines the coefficients for the system b(z)/a(z) given an approximate impulse response x, as well as the desired number of zeros and poles. This function identifies an unknown system based on both input and output sequences that describe the system's behavior, or just the impulse response of the system. In its default mode, stmcb works like prony.

[b,a] = stmcb(x,3,3)
b =
    0.9567   -0.5181    0.5702   -0.5471
a =
    1.0000   -0.2384    0.5234   -0.3065

stmcb also finds systems that match given input and output sequences:

y = filter(1,[1 1],x);  % Create an output signal.
[b,a] = stmcb(y,x,0,1)
b = 
     1.0000
a =
     1     1

In this example, stmcb correctly identifies the system used to create y from x.

The Steiglitz-McBride method is a fast iterative algorithm that solves for the numerator and denominator coefficients simultaneously in an attempt to minimize the signal error between the filter output and the given output signal. This algorithm usually converges rapidly, but might not converge if the model order is too large. As for prony, stmcb's resulting filter is not necessarily stable due to its exact modeling approach.

stmcb provides control over several important algorithmic parameters; modify these parameters if you are having trouble modeling the data. To change the number of iterations from the default of five and provide an initial estimate for the denominator coefficients:

n = 10;            % Number of iterations
a = lpc(x,3);      % Initial estimates for denominator
[b,a] = stmcb(x,3,3,n,a);

The function uses an all-pole model created with prony as an initial estimate when you do not provide one of your own.

To compare the functions lpc, prony, and stmcb, compute the signal error in each case:

a1 = lpc(x,3);
[b2,a2] = prony(x,3,3);
[b3,a3] = stmcb(x,3,3);
[x-impz(1,a1,10)  x-impz(b2,a2,10)  x-impz(b3,a3,10)]
ans =
   -0.0433         0   -0.0000
   -0.0240         0    0.0234
   -0.0040         0   -0.0778
   -0.0448   -0.0000    0.0498
   -0.2130   -0.1303   -0.0742
    0.1545    0.1655    0.1270
    0.1426    0.1404    0.1055
    0.0068    0.0188    0.0465
    0.0329    0.0376    0.0530
    0.0108    0.0081   -0.0162
sum(ans.^2)
ans =
    0.0953    0.0659    0.0471

In comparing modeling capabilities for a given order IIR model, the last result shows that for this example, stmcb performs best, followed by prony, then lpc. This relative performance is typical of the modeling functions.

Parametric Modeling Frequency-Domain Based Modeling