Frequency-Domain Based Modeling :: Special Topics (Signal Processing Toolbox)

Signal Processing Toolbox

Frequency-Domain Based Modeling

The invfreqs and invfreqz functions implement the inverse operations of freqs and freqz; they find an analog or digital transfer function of a specified order that matches a given complex frequency response. Though the following examples demonstrate invfreqz, the discussion also applies to invfreqs.

To recover the original filter coefficients from the frequency response of a simple digital filter:

[b,a] = butter(4,0.4)    % Design Butterworth lowpass
b =
    0.0466    0.1863    0.2795    0.1863    0.0466
a =
    1.0000   -0.7821    0.6800   -0.1827    0.0301
[h,w] = freqz(b,a,64);         % Compute frequency response
[b4,a4] = invfreqz(h,w,4,4)    % Model: n = 4, m = 4
b4 =
    0.0466    0.1863    0.2795    0.1863    0.0466
a4 =
    1.0000   -0.7821    0.6800   -0.1827    0.0301

The vector of frequencies w has the units in rad/sample, and the frequencies need not be equally spaced. invfreqz finds a filter of any order to fit the frequency data; a third-order example is

[b4,a4] = invfreqz(h,w,3,3)   % Find third-order IIR
b4 =
    0.0464    0.1785    0.2446    0.1276
a4 =
    1.0000   -0.9502    0.7382   -0.2006

Both invfreqs and invfreqz design filters with real coefficients; for a data point at positive frequency f, the functions fit the frequency response at both f and -f.

By default invfreqz uses an equation error method to identify the best model from the data. This finds b and a in

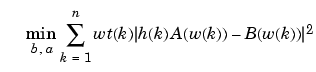
by creating a system of linear equations and solving them with the MATLAB \ operator. Here A(w(k)) and B(w(k)) are the Fourier transforms of the polynomials a and b respectively at the frequency w(k), and n is the number of frequency points (the length of h and w). wt(k) weights the error relative to the error at different frequencies. The syntax

```
invfreqz(h,w,n,m,wt)
```

includes a weighting vector. In this mode, the filter resulting from invfreqz is not guaranteed to be stable.

invfreqz provides a superior ("output-error") algorithm that solves the direct problem of minimizing the weighted sum of the squared error between the actual frequency response points and the desired response

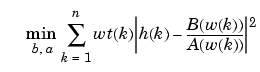
To use this algorithm, specify a parameter for the iteration count after the weight vector parameter:

wt = ones(size(w));    % Create unity weighting vector
[b30,a30] = invfreqz(h,w,3,3,wt,30)  % 30 iterations
b30 =
    0.0464    0.1829    0.2572    0.1549
a30 =
    1.0000   -0.8664    0.6630   -0.1614

The resulting filter is always stable.

Graphically compare the results of the first and second algorithms to the original Butterworth filter with FVTool (and select the Magnitude and Phase Responses):

```
fvtool(b,a,b4,a4,b30,a30)
```

To verify the superiority of the fit numerically, type

sum(abs(h-freqz(b4,a4,w)).^2)   % Total error, algorithm 1
ans =
    0.0200
sum(abs(h-freqz(b30,a30,w)).^2) % Total error, algorithm 2
ans =
    0.0096

Time-Domain Based Modeling Resampling