| Signal Processing Toolbox | |
The goal of spectral estimation is to describe the distribution (over frequency) of the power contained in a signal, based on a finite set of data. Estimation of power spectra is useful in a variety of applications, including the detection of signals buried in wide-band noise.
The power spectrum of a stationary random process xn is mathematically related to the correlation sequence by the discrete-time Fourier transform. In terms of normalized frequency, this is given by
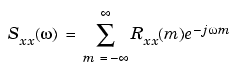
This can be written as a function of physical frequency f (e.g., in hertz) by using the relation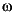 
= 2
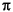f/fs, where fs is the sampling frequency.
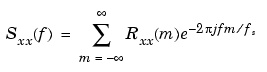
The correlation sequence can be derived from the power spectrum by use of the inverse discrete-time Fourier transform:
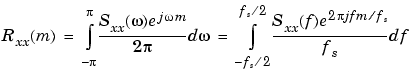
The average power of the sequence xn over the entire Nyquist interval is represented by
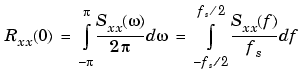
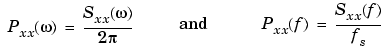
from the above expression are defined as the power spectral density (PSD) of the stationary random signal xn.
The average power of a signal over a particular frequency band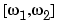 
, 
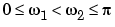, can be found by integrating the PSD over that band:
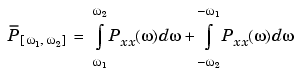
You can see from the above expression that Pxx(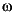) represents the power content of a signal in an infinitesimal frequency band, which is why it is called the power spectral density.
The units of the PSD are power (e.g., watts) per unit of frequency. In the case of Pxx(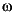), this is watts/radian/sample or simply watts/radian. In the case of Pxx(f), the units are watts/hertz. Integration of the PSD with respect to frequency yields units of watts, as expected for the average power 
.
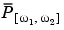For real signals, the PSD is symmetric about DC, and thus Pxx(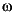) for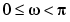 
is sufficient to completely characterize the PSD. However, to obtain the average power over the entire Nyquist interval, it is necessary to introduce the concept of the one-sided PSD.
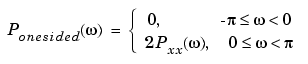
The average power of a signal over the frequency band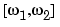 
, 
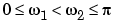, can be computed using the one-sided PSD as
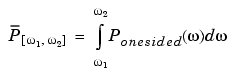
| | Multiple Channels | Spectral Estimation Method | |
© 1994-2005 The MathWorks, Inc.