Signal Processing Toolbox

Spectral Estimation Method

The various methods of spectrum estimation available in the Signal Processing Toolbox are categorized as follows:

• Nonparametric methods
• Parametric methods
• Subspace methods

Nonparametric methods are those in which the PSD is estimated directly from the signal itself. The simplest such method is the periodogram. An improved version of the periodogram is Welch's method [8]. A more modern nonparametric technique is the multitaper method (MTM).

Parametric methods are those in which the PSD is estimated from a signal that is assumed to be output of a linear system driven by white noise. Examples are the Yule-Walker autoregressive (AR) method and the Burg method. These methods estimate the PSD by first estimating the parameters (coefficients) of the linear system that hypothetically "generates" the signal. They tend to produce better results than classical nonparametric methods when the data length of the available signal is relatively short.

Subspace methods, also known as high-resolution methods or super-resolution methods, generate frequency component estimates for a signal based on an eigenanalysis or eigendecomposition of the correlation matrix. Examples are the multiple signal classification (MUSIC) method or the eigenvector (EV) method. These methods are best suited for line spectra -- that is, spectra of sinusoidal signals -- and are effective in the detection of sinusoids buried in noise, especially when the signal to noise ratios are low.

All three categories of methods are listed in the table below with the corresponding toolbox function and spectrum object names. More information about each function is on the corresponding function reference page. See Parametric Modeling for details about lpc and other parametric estimation functions.

.

Method	Description	Functions
Periodogram	Power spectral density estimate	spectrum.periodogram, periodogram
Welch	Averaged periodograms of overlapped, windowed signal sections	spectrum.welch, pwelch, cpsd, tfestimate, mscohere
Multitaper)	Spectral estimate from combination of multiple orthogonal windows (or "tapers")	spectrum.mtm, pmtm
Yule-Walker AR	Autoregressive (AR) spectral estimate of a time-series from its estimated autocorrelation function	spectrum.yulear, pyulear
Burg	Autoregressive (AR) spectral estimation of a time-series by minimization of linear prediction errors	spectrum.burg, pburg
Covariance	Autoregressive (AR) spectral estimation of a time-series by minimization of the forward prediction errors	spectrum.cov, pcov
Modified Covariance	Autoregressive (AR) spectral estimation of a time-series by minimization of the forward and backward prediction errors	spectrum.mcov, pmcov
MUSIC	Multiple signal classification	spectrum.music, pmusic
Eigenvector	Pseudospectrum estimate	spectrum.eigenvector, peig

Nonparametric Methods

The following sections discuss the periodogram, modified periodogram, Welch, and multitaper methods of nonparametric estimation, along with the related CPSD function, transfer function estimate, and coherence function.

Periodogram

One way of estimating the power spectrum of a process is to simply find the discrete-time Fourier transform of the samples of the process (usually done on a grid with an FFT) and take the magnitude squared of the result. This estimate is called the periodogram.

The periodogram estimate of the PSD of a length-L signal x_L[n] is

where

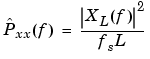
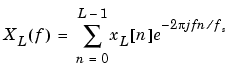
The actual computation of X_L(f) can be performed only at a finite number of frequency points, N, and usually employs the FFT. In practice, most implementations of the periodogram method compute the N-point PSD estimate

where

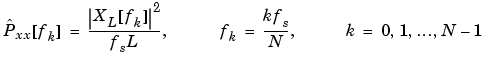
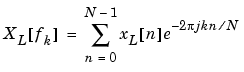
It is wise to choose N > L so that N is the next power of two larger than L. To evaluate X_L[f_k], we simply pad x_L[n] with zeros to length N. If L > N, we must wrap x_L[n] modulo-N prior to computing X_L[f_k].

As an example, consider the following 1001-element signal xn, which consists of two sinusoids plus noise:

• randn('state',0);
  fs = 1000;           % Sampling frequency
  t = (0:fs)/fs;       % One second worth of samples
  A = [1 2];           % Sinusoid amplitudes (row vector)
  f = [150;140];       % Sinusoid frequencies (column vector)
  xn = A*sin(2*pi*f*t) + 0.1*randn(size(t));
  

Note    The three last lines illustrate a convenient and general way to express the sum of sinusoids. Together they are equivalent to    xn = sin(2*pi*150*t) + 2*sin(2*pi*140*t) + 0.1*randn(size(t));

The periodogram estimate of the PSD can be computed by creating a periodogram object

• Hs = spectrum.periodogram('Hamming');
  

and a plot of the estimate can be displayed with the psd method:

• psd(Hs,xn,'Fs',fs,'NFFT',1024,'SpectrumType','twosided')
  
  
  

The average power can be computed by approximating the integral with the following sum:

• [Pxx,F] = psd(Hs,xn,fs,'twosided');
  Pow = (fs/length(Pxx)) * sum(Pxx)
  
  Pow =
      2.5059
  

You can also compute the average power from the one-sided PSD estimate:

• [Pxxo,F] = psd(Hs,xn,fs,'onesided');
  Pow = (fs/(2*length(Pxxo))) * sum(Pxxo)
  
  Pow =
      2.5011
  

Spectral Analysis

Performance of the Periodogram

© 1994-2005 The MathWorks, Inc.