tf2zpk (Signal Processing Toolbox)

Signal Processing Toolbox

tf2zpk

Convert transfer function filter parameters to zero-pole-gain form

Syntax

```
[z,p,k] = tf2zpk(b,a) 
```

Description

tf2zpk finds the zeros, poles, and gains of a discrete-time transfer function.

Note You should use tf2zpk when working with transfer functions expressed in inverse powers (1 + z^-1 + z^-2), which is how transfer functions are usually expressed in DSP. A similar function, tf2zp, is more useful for working with positive powers (s² + s + 1), such as in continuous-time transfer functions.

[z,p,k] = tf2zpk(b,a) finds the matrix of zeros z, the vector of poles p, and the associated vector of gains k from the transfer function parameters b and a:

The numerator polynomials are represented as columns of the matrix b.
The denominator polynomial is represented in the vector a.

Given a single-input, multiple output (SIMO) discrete-time system in polynomial transfer function form

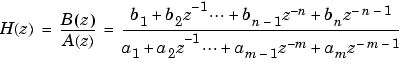
you can use the output of tf2zpk to produce the single-input, multioutput (SIMO) factored transfer function form

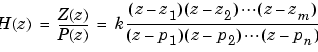
The following describes the input and output arguments for tf2zpk:

The vector a specifies the coefficients of the denominator polynomial A(z) in descending powers of z.
The ith row of the matrix b represents the coefficients of the ith numerator polynomial (the ith row of B(s) or B(z)). Specify as many rows of b as there are outputs.
The zero locations are returned in the columns of the matrix z, with as many columns as there are rows in b.
The pole locations are returned in the column vector p and the gains for each numerator transfer function in the vector k.

Examples

Find the poles, zeros, and gain of a Butterworth filter:

[b,a] = butter(3,.4);
[z,p,k] = tf2zpk(b,a)
z =
  -1.0000          
  -1.0000 + 0.0000i
  -1.0000 - 0.0000i

p =
   0.2094 + 0.5582i
   0.2094 - 0.5582i
   0.1584          

k =
    0.0985

See Also

sos2zp, ss2zp, tf2sos, tf2ss, tf2zp, zp2tf

tf2zp tfestimate