

| Wavelet Toolbox |   |
Biorthogonal wavelet filter set
Syntax
[Lo_D,Hi_D,Lo_R,Hi_R] = biorfilt(DF,RF) [Lo_D1,Hi_D1,Lo_R1,Hi_R1,Lo_D2,Hi_D2,Lo_R2,Hi_R2] = biorfilt(DF,RF,'8')
Description
The biorfilt command returns either four or eight filters associated with biorthogonal wavelets.
[Lo_D,Hi_D,Lo_R,Hi_R] = biorfilt(DF,RF) computes four filters associated with the biorthogonal wavelet specified by decomposition filter DF and reconstruction filter RF. These filters are
|
Decomposition low-pass filter |
|
Decomposition high-pass filter |
|
Reconstruction low-pass filter |
|
Reconstruction high-pass filter |
[Lo_D1,Hi_D1,Lo_R1,Hi_R1,Lo_D2,Hi_D2,Lo_R2,Hi_R2] = biorfilt(DF,RF,'8') returns eight filters, the first four associated with the decomposition wavelet, and the last four associated with the reconstruction wavelet.
It is well known in the subband filtering community that if the same FIR filters are used for reconstruction and decomposition, then symmetry and exact reconstruction are incompatible (except with the Haar wavelet). Therefore, with biorthogonal filters, two wavelets are introduced instead of just one:
One wavelet, 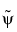 , is used in the analysis, and the coefficients of a signal s are
, is used in the analysis, and the coefficients of a signal s are
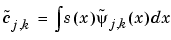
The other wavelet, 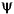 , is used in the synthesis:
, is used in the synthesis:
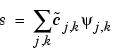
Furthermore, the two wavelets are related by duality in the following sense:
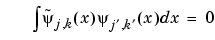 as soon as
as soon as 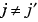 or
or 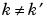 and
and
It becomes apparent, as A. Cohen pointed out in his thesis (p. 110), that "the useful properties for analysis (e.g., oscillations, null moments) can be concentrated in the 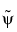 function; whereas, the interesting properties for synthesis (regularity) are assigned to the
function; whereas, the interesting properties for synthesis (regularity) are assigned to the 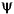 function. The separation of these two tasks proves very useful."
function. The separation of these two tasks proves very useful."
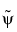 and
and 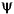 can have very different regularity properties,
can have very different regularity properties, 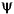 being more regular than
being more regular than 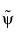 .
.
The 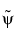 ,
, 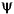 ,
, 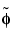 and
and 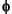 functions are zero outside a segment.
functions are zero outside a segment.
Examples
% Compute the four filters associated with spline biorthogonal
% wavelet 3.5: bior3.5.
% Find the two scaling filters associated with bior3.5.
[Rf,Df] = biorwavf('bior3.5');
% Compute the four filters needed.
[Lo_D,Hi_D,Lo_R,Hi_R] = biorfilt(Df,Rf);
subplot(221); stem(Lo_D);
title('Dec. low-pass filter bior3.5');
subplot(222); stem(Hi_D);
title('Dec. high-pass filter bior3.5');
subplot(223); stem(Lo_R);
title('Rec. low-pass filter bior3.5');
subplot(224); stem(Hi_R);
title('Rec. high-pass filter bior3.5');
% Editing some graphical properties,
% the following figure is generated.
% Orthogonality by dyadic translation is lost.
nzer = [Lo_D 0 0]*[0 0 Lo_D]'
nzer =
-0.6881
nzer = [Hi_D 0 0]*[0 0 Hi_D]'
nzer =
0.1875
% But using duality we have:
zer = [Lo_D 0 0]*[0 0 Lo_R]'
zer =
-2.7756e-17
zer = [Hi_D 0 0]*[0 0 Hi_R]'
zer =
2.7756e-17
% But, perfect reconstruction via DWT is preserved.
x = randn(1,500);
[a,d] = dwt(x,Lo_D,Hi_D);
xrec = idwt(a,d,Lo_R,Hi_R);
err = norm(x-xrec)
err =
5.0218e-15
% High and low frequency illustration.
fftld = fft(Lo_D); ffthd = fft(Hi_D);
freq = [1:length(Lo_D)]/length(Lo_D);
subplot(221); plot(freq,abs(fftld),freq,abs(ffthd));
title('Transfer modulus for dec. filters')
fftlr = fft(Lo_R); ffthr = fft(Hi_R);
freq = [1:length(Lo_R)]/length(Lo_R);
subplot(222); plot(freq,abs(fftlr),freq,abs(ffthr));
title('Transfer modulus for rec. filters')
subplot(223); plot(freq, abs(fftlr.*fftld + ffthd.*ffthr));
title('One biorthogonality condition')
xlabel('|fft(Lo_R)fft(Lo_D) + fft(Hi_R)fft(Hi_D)| = 2')
% Editing some graphical properties,
% the following figure is generated.
References
Cohen, A. (1992), "Ondelettes, analyses multirésolution et traitement numérique du signal," Ph. D. Thesis, University of Paris IX, DAUPHINE.
Daubechies, I. (1992), Ten lectures on wavelets, CBMS-NSF conference series in applied mathematics. SIAM Ed.
 | besttree | biorwavf |  |
© 1994-2005 The MathWorks, Inc.