Wavelet Toolbox

Multistep Decomposition and Reconstruction

A multistep analysis-synthesis process can be represented as

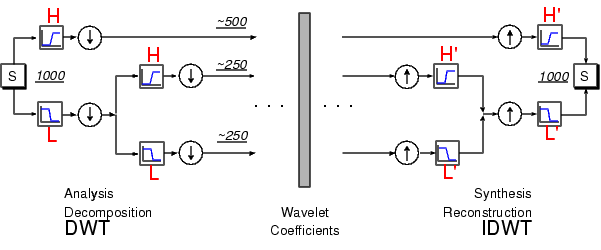
This process involves two aspects: breaking up a signal to obtain the wavelet coefficients, and reassembling the signal from the coefficients.

We've already discussed decomposition and reconstruction at some length. Of course, there is no point breaking up a signal merely to have the satisfaction of immediately reconstructing it. We may modify the wavelet coefficients before performing the reconstruction step. We perform wavelet analysis because the coefficients thus obtained have many known uses, de-noising and compression being foremost among them.

But wavelet analysis is still a new and emerging field. No doubt, many uncharted uses of the wavelet coefficients lie in wait. The Wavelet Toolbox can be a means of exploring possible uses and hitherto unknown applications of wavelet analysis. Explore the toolbox functions and see what you discover.

Relationship of Filters to Wavelet Shapes

Wavelet Packet Analysis

© 1994-2005 The MathWorks, Inc.