Wavelet Toolbox

Relationship of Filters to Wavelet Shapes

In the section Reconstruction Filters, we spoke of the importance of choosing the right filters. In fact, the choice of filters not only determines whether perfect reconstruction is possible, it also determines the shape of the wavelet we use to perform the analysis.

To construct a wavelet of some practical utility, you seldom start by drawing a waveform. Instead, it usually makes more sense to design the appropriate quadrature mirror filters, and then use them to create the waveform. Let's see how this is done by focusing on an example.

Consider the low-pass reconstruction filter (L') for the db2 wavelet.

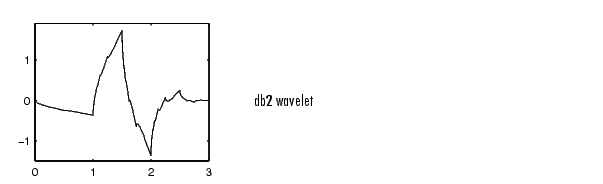
The filter coefficients can be obtained from the dbaux command:

• Lprime = dbaux(2)
  
  Lprime =
      0.3415    0.5915    0.1585   -0.0915
  

If we reverse the order of this vector (see wrev), and then multiply every even sample by -1, we obtain the high-pass filter H':

• Hprime =
     -0.0915   -0.1585    0.5915   -0.3415
  

Next, upsample Hprime by two (see dyadup), inserting zeros in alternate positions:

• HU =
      -0.0915         0   -0.1585         0    0.5915         0   -0.3415       0
  

Finally, convolve the upsampled vector with the original low-pass filter:

• H2 = conv(HU,Lprime);
  plot(H2)
  

If we iterate this process several more times, repeatedly upsampling and convolving the resultant vector with the four-element filter vector Lprime, a pattern begins to emerge.

The curve begins to look progressively more like the db2 wavelet. This means that the wavelet's shape is determined entirely by the coefficients of the reconstruction filters.

This relationship has profound implications. It means that you cannot choose just any shape, call it a wavelet, and perform an analysis. At least, you can't choose an arbitrary wavelet waveform if you want to be able to reconstruct the original signal accurately. You are compelled to choose a shape determined by quadrature mirror decomposition filters.

The Scaling Function

We've seen the interrelation of wavelets and quadrature mirror filters. The wavelet function 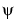is determined by the high-pass filter, which also produces the details of the wavelet decomposition.

There is an additional function associated with some, but not all, wavelets. This is the so-called scaling function, 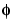. The scaling function is very similar to the wavelet function. It is determined by the low-pass quadrature mirror filters, and thus is associated with the approximations of the wavelet decomposition.

In the same way that iteratively upsampling and convolving the high-pass filter produces a shape approximating the wavelet function, iteratively upsampling and convolving the low-pass filter produces a shape approximating the scaling function.

Reconstructing Approximations and Details

Multistep Decomposition and Reconstruction

© 1994-2005 The MathWorks, Inc.