Wavelet Toolbox

What Can Wavelet Analysis Do?

One major advantage afforded by wavelets is the ability to perform local analysis -- that is, to analyze a localized area of a larger signal.

Consider a sinusoidal signal with a small discontinuity -- one so tiny as to be barely visible. Such a signal easily could be generated in the real world, perhaps by a power fluctuation or a noisy switch.

A plot of the Fourier coefficients (as provided by the fft command) of this signal shows nothing particularly interesting: a flat spectrum with two peaks representing a single frequency. However, a plot of wavelet coefficients clearly shows the exact location in time of the discontinuity.

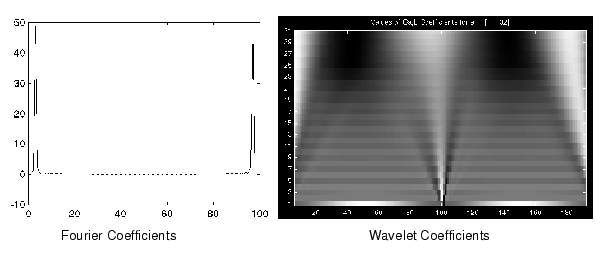
Wavelet analysis is capable of revealing aspects of data that other signal analysis techniques miss, aspects like trends, breakdown points, discontinuities in higher derivatives, and self-similarity. Furthermore, because it affords a different view of data than those presented by traditional techniques, wavelet analysis can often compress or de-noise a signal without appreciable degradation.

Indeed, in their brief history within the signal processing field, wavelets have already proven themselves to be an indispensable addition to the analyst's collection of tools and continue to enjoy a burgeoning popularity today.

Wavelet Analysis

What Is Wavelet Analysis?

© 1994-2005 The MathWorks, Inc.