Wavelet Toolbox

What Is Wavelet Analysis?

Now that we know some situations when wavelet analysis is useful, it is worthwhile asking "What is wavelet analysis?" and even more fundamentally, "What is a wavelet?"

A wavelet is a waveform of effectively limited duration that has an average value of zero.

Compare wavelets with sine waves, which are the basis of Fourier analysis. Sinusoids do not have limited duration -- they extend from minus to plus infinity. And where sinusoids are smooth and predictable, wavelets tend to be irregular and asymmetric.

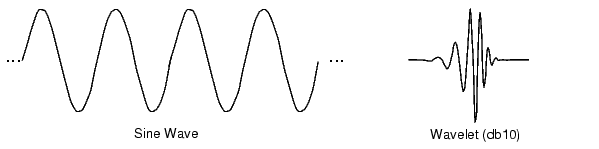
Fourier analysis consists of breaking up a signal into sine waves of various frequencies. Similarly, wavelet analysis is the breaking up of a signal into shifted and scaled versions of the original (or mother) wavelet.

Just looking at pictures of wavelets and sine waves, you can see intuitively that signals with sharp changes might be better analyzed with an irregular wavelet than with a smooth sinusoid, just as some foods are better handled with a fork than a spoon.

It also makes sense that local features can be described better with wavelets that have local extent.

Number of Dimensions

Thus far, we've discussed only one-dimensional data, which encompasses most ordinary signals. However, wavelet analysis can be applied to two-dimensional data (images) and, in principle, to higher dimensional data.

This toolbox uses only one- and two-dimensional analysis techniques.

What Can Wavelet Analysis Do?

The Continuous Wavelet Transform

© 1994-2005 The MathWorks, Inc.