Wavelet Toolbox

Scaling

We've already alluded to the fact that wavelet analysis produces a time-scale view of a signal, and now we're talking about scaling and shifting wavelets. What exactly do we mean by scale in this context?

Scaling a wavelet simply means stretching (or compressing) it.

To go beyond colloquial descriptions such as "stretching," we introduce the scale factor, often denoted by the letter 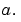If we're talking about sinusoids, for example, the effect of the scale factor is very easy to see:

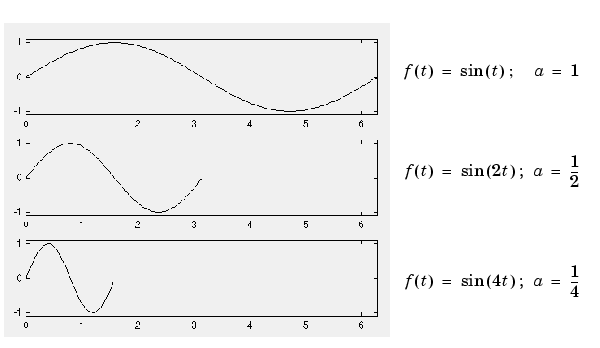
The scale factor works exactly the same with wavelets. The smaller the scale factor, the more "compressed" the wavelet.

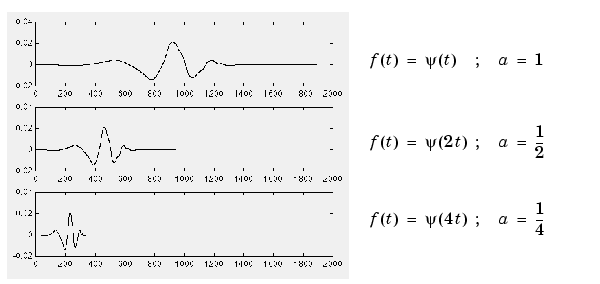
It is clear from the diagrams that, for a sinusoid 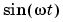, the scale factor 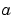is related (inversely) to the radian frequency 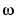. Similarly, with wavelet analysis, the scale is related to the frequency of the signal. We'll return to this topic later.

The Continuous Wavelet Transform

Shifting

© 1994-2005 The MathWorks, Inc.