Wavelet Toolbox

The Continuous Wavelet Transform

Mathematically, the process of Fourier analysis is represented by the Fourier transform:

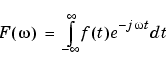
which is the sum over all time of the signal f(t) multiplied by a complex exponential. (Recall that a complex exponential can be broken down into real and imaginary sinusoidal components.)

The results of the transform are the Fourier coefficients 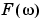, which when multiplied by a sinusoid of frequency 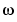yield the constituent sinusoidal components of the original signal. Graphically, the process looks like

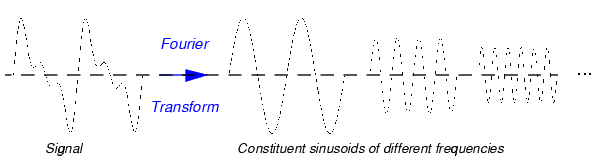
Similarly, the continuous wavelet transform (CWT) is defined as the sum over all time of the signal multiplied by scaled, shifted versions of the wavelet function :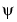

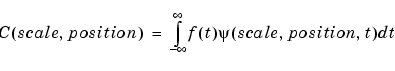
The results of the CWT are many wavelet coefficients C, which are a function of scale and position.

Multiplying each coefficient by the appropriately scaled and shifted wavelet yields the constituent wavelets of the original signal:

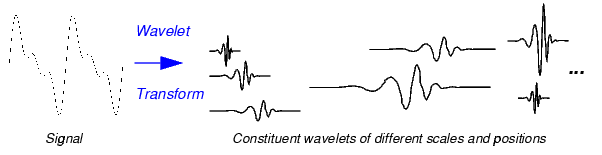
What Is Wavelet Analysis?

Scaling

© 1994-2005 The MathWorks, Inc.