Wavelet Toolbox

Reconstructing Approximations and Details

We have seen that it is possible to reconstruct our original signal from the coefficients of the approximations and details.

It is also possible to reconstruct the approximations and details themselves from their coefficient vectors. As an example, let's consider how we would reconstruct the first-level approximation A1 from the coefficient vector cA1.

We pass the coefficient vector cA1 through the same process we used to reconstruct the original signal. However, instead of combining it with the level-one detail cD1, we feed in a vector of zeros in place of the detail coefficients vector:

The process yields a reconstructed approximation A1, which has the same length as the original signal S and which is a real approximation of it.

Similarly, we can reconstruct the first-level detail D1, using the analogous process:

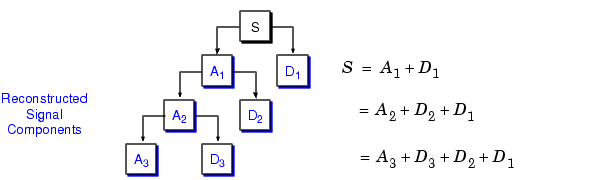
The reconstructed details and approximations are true constituents of the original signal. In fact, we find when we combine them that

Note that the coefficient vectors cA1 and cD1 -- because they were produced by downsampling and are only half the length of the original signal -- cannot directly be combined to reproduce the signal. It is necessary to reconstruct the approximations and details before combining them.

Extending this technique to the components of a multilevel analysis, we find that similar relationships hold for all the reconstructed signal constituents. That is, there are several ways to reassemble the original signal:

Reconstruction Filters

Relationship of Filters to Wavelet Shapes

© 1994-2005 The MathWorks, Inc.