Wavelet Toolbox

Wavelet Applications

Wavelets have scale aspects and time aspects, consequently every application has scale and time aspects. To clarify them we try to untangle the aspects somewhat arbitrarily.

For scale aspects, we present one idea around the notion of local regularity. For time aspects, we present a list of domains. When the decomposition is taken as a whole, the de-noising and compression processes are center points.

Scale Aspects

As a complement to the spectral signal analysis, new signal forms appear. They are less regular signals than the usual ones.

The cusp signal presents a very quick local variation. Its equation is 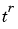with t close to 0 and 0 < r < 1. The lower r the sharper the signal.

To illustrate this notion physically, imagine you take a piece of aluminum foil; The surface is very smooth, very regular. You first crush it into a ball, and then you spread it out so that it looks like a surface. The asperities are clearly visible. Each one represents a two-dimension cusp and analog of the one dimensional cusp. If you crush again the foil, more tightly, in a more compact ball, when you spread it out, the roughness increases and the regularity decreases.

Several domains use the wavelet techniques of regularity study:

• Biology for cell membrane recognition, to distinguish the normal from the pathological membranes
• Metallurgy for the characterization of rough surfaces
• Finance (which is more surprising), for detecting the properties of quick variation of values
• In Internet traffic description, for designing the services size

Time Aspects

Let's switch to time aspects. The main goals are

• Rupture and edges detection
• Study of short-time phenomena as transient processes

As domain applications, we get

• Industrial supervision of gear-wheel
• Checking undue noises in craned or dented wheels, and more generally in nondestructive control quality processes
• Detection of short pathological events as epileptic crises or normal ones as evoked potentials in EEG (medicine)
• SAR imagery
• Automatic target recognition
• Intermittence in physics

Wavelet Decomposition as a Whole

Many applications use the wavelet decomposition taken as a whole. The common goals concern the signal or image clearance and simplification, which are parts of de-noising or compression.

We find many published papers in oceanography and earth studies.

One of the most popular successes of the wavelets is the compression of FBI fingerprints.

When trying to classify the applications by domain, it is almost impossible to sum up several thousand papers written within the last 15 years. Moreover, it is difficult to get information on real-world industrial applications from companies. They understandably protect their own information.

Some domains are very productive. Medicine is one of them. We can find studies on micro-potential extraction in EKGs, on time localization of His bundle electrical heart activity, in ECG noise removal. In EEGs, a quick transitory signal is drowned in the usual one. The wavelets are able to determine if a quick signal exists, and if so, can localize it. There are attempts to enhance mammograms to discriminate tumors from calcifications.

Another prototypical application is a classification of Magnetic Resonance Spectra. The study concerns the influence of the fat we eat on our body fat. The type of feeding is the basic information and the study is intended to avoid taking a sample of the body fat. Each Fourier spectrum is encoded by some of its wavelet coefficients. A few of them are enough to code the most interesting features of the spectrum. The classification is performed on the coded vectors.

Platform-Specific Details

Fourier Analysis

© 1994-2005 The MathWorks, Inc.