Wavelet Toolbox

Some Interesting Subtrees

Using wavelet packets requires tree-related actions and labeling. The implementation of the user interface is built around this consideration. For more information on the technical details, see the reference pages.

The complete binary tree of depth D corresponding to a wavelet packet decomposition tree developed at level D is denoted by WPT.

We have the following interesting subtrees:

Decomposition Tree	Subtree Such That the Set of Leaves Is a Basis
Wavelet packets decomposition tree	Complete binary tree: WPT of depth D
Wavelet packets optimal decomposition tree	Binary subtree of WPT
Wavelet packets best-level tree	Complete binary subtree of WPT
Wavelet decomposition tree	Left unilateral binary subtree of WPT of depth D
Wavelet best-basis tree	Left unilateral binary subtree of WPT

We deduce the following definitions of optimal decompositions, with respect to an entropy criterion E.

Decompositions	Optimal Decomposition	Best-Level Decomposition
Wavelet packet decompositions	Search among 2D trees	Search among D trees
Wavelet decompositions	Search among D trees	Search among D trees

For any nonterminal node, we use the following basic step to find the optimal subtree with respect to a given entropy criterion E (where Eopt denotes the optimal entropy value).

Entropy Condition	Action on Tree and on Entropy Labeling

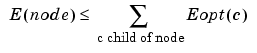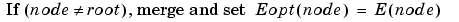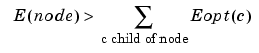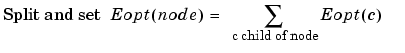with the natural initial condition on the reference tree, Eopt(t) = E(t) for each terminal node t.

Choosing the Optimal Decomposition

Wavelet Packets 2-D Decomposition Structure

© 1994-2005 The MathWorks, Inc.