| Wavelet Toolbox |
  |
One-Dimensional Wavelet Capabilities
Basic one-dimensional objects.
|
Objects
|
Description
|
Signal in original time
|
s
Ak, 0  k k  j j
Dk, 1  k k  j j
|
Original signal
Approximation at level k
Detail at level k
|
Coefficients in scale-related time
|
cAk, 1  k k  j j
cDk, 1  k k  j j
[cAj, cDj, ..., cD1]
|
Approximation coefficients at level k
Detail coefficients at level k
Wavelet decomposition at level j, j 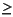 1 1
|
Analysis-decomposition capabilities.
Purpose
|
Input
|
Output
|
M-File
|
Single-level decomposition
|
s
|
cA1, cD1
|
dwt
|
Single-level decomposition
|
cAj
|
cAj+1, cDj+1
|
dwt
|
Decomposition
|
s
|
[cAj, cDj, ..., cD1]
|
wavedec
|
Synthesis-reconstruction capabilities.
Purpose
|
Input
|
Output
|
M-File
|
Single-level reconstruction
|
cA1, cD1
|
s or A0
|
idwt
|
Single-level reconstruction
|
cAj+1, cDj+1
|
cAj
|
idwt
|
Full reconstruction
|
[cAj, cDj, ..., cD1]
|
s or A0
|
waverec
|
Selective reconstruction
|
[cAj, cDj, ..., cD1]
|
Al, Dm
|
wrcoef
|
Decomposition structure utilities. .
Purpose
|
Input
|
Output
|
M-File
|
Extraction of detail coefficients
|
[cAj, cDj, ..., cD1]
|
cDk,
1  k k  j j
|
detcoef
|
Extraction of approximation coefficients
|
[cAj, cDj, ..., cD1]
|
cAk,
0 k k  j j
|
appcoef
|
Recomposition of the decomposition structure
|
[cAj, cDj, ..., cD1]
|
[cAk, cDk, ..., cD1]
1  k k  j j
|
upwlev
|
To illustrate the command line mode for one-dimensional capabilities, see the section One-Dimensional Analysis Using the Command Line.
 | Why Does Such an Algorithm Exist? | | Two-Dimensional Wavelet Capabilities |  |
© 1994-2005 The MathWorks, Inc.





