

| Wavelet Toolbox |   |
Why Does Such an Algorithm Exist?
The previous paragraph describes algorithms designed for finite-length signals or images. To understand the rationale, we must consider infinite-length signals. The methods for the extension of a given finite-length signal are described in the section Dealing with Border Distortion.
Let us denote h = Lo_R and g = Hi_R and focus on the one-dimensional case.
We first justify how to go from level j to level j+1, for the approximation vector. This is the main step of the decomposition algorithm for the computation of the approximations. The details are calculated in the same way using the filter g instead of filter h.
Let 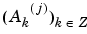 be the coordinates of the vector Aj:
be the coordinates of the vector Aj:
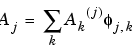
and 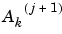 the coordinates of the vector Aj+1:
the coordinates of the vector Aj+1:
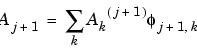
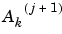 is calculated using the formula
is calculated using the formula
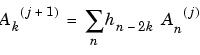
This formula resembles a convolution formula.
The computation is very simple.
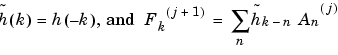
The sequence 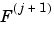 is the filtered output of the sequence
is the filtered output of the sequence 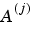 by the filter
by the filter 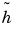 .
.
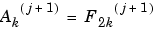
We have to take the even index values of F. This is downsampling.
The sequence 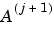 is the downsampled version of the sequence
is the downsampled version of the sequence 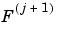 .
.
The initialization is carried out using 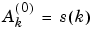 , where s(k) is the signal value at time k.
, where s(k) is the signal value at time k.
There are several reasons for this surprising result, all of which are linked to the multiresolution situation and to a few of the properties of the functions 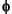 j,k and
j,k and 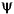 j,k.
j,k.
Let us now describe some of them.
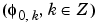 is formed of orthonormal functions. As a consequence for any j, the family
is formed of orthonormal functions. As a consequence for any j, the family 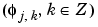 is orthonormal.
is orthonormal.
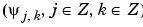 is orthonormal.
is orthonormal.
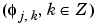 are orthogonal to
are orthogonal to 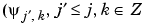 .
.
Twin-Scale Relation for 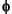 | |
|
|
This relation introduces the algorithm's h filter (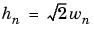 ). For more information, see the section Filters Used to Calculate the DWT and IDWT.
). For more information, see the section Filters Used to Calculate the DWT and IDWT.
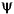 and
and 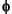 functions. Between two successive scales, we have the following twin-scale fundamental relation.
functions. Between two successive scales, we have the following twin-scale fundamental relation.Twin-Scale Relation Between 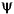 and and 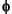 | |
|
|
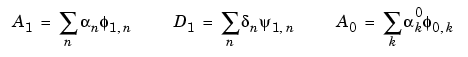
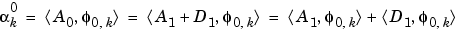
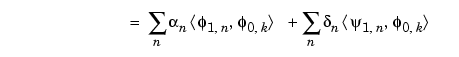
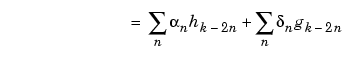
We will focus our study on the first sum
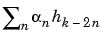 ; the second sum
; the second sum
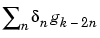 is handled in a similar manner.
is handled in a similar manner.
The calculations are easily organized if we note that (taking k = 0 in the previous formulas, makes things simpler)
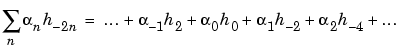
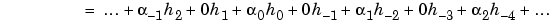
If we transform the (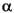 n) sequence into a new sequence
n) sequence into a new sequence 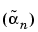 defined by
defined by
..., 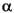 -1, 0,
-1, 0, 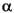 0, 0,
0, 0, 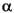 1, 0,
1, 0, 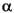 2, 0, ... that is precisely
2, 0, ... that is precisely
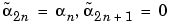
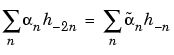
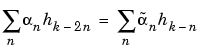
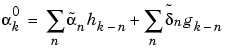
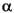 and
and 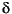 sequences by upsampled versions
sequences by upsampled versions 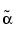 and
and 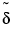 inserting zeros.
inserting zeros.
 | Algorithms | One-Dimensional Wavelet Capabilities |  |
© 1994-2005 The MathWorks, Inc.