Wavelet Toolbox

Discrete Stationary Wavelet Transform (SWT)

We know that the classical DWT suffers a drawback: the DWT is not a time- invariant transform.

This means that, even with periodic signal extension, the DWT of a translated version of a signal X is not, in general, the translated version of the DWT of X.
How to restore the translation invariance, which is a desirable property lost by the classical DWT?

The idea is to average some slightly different DWT, called 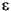-decimated DWT, to define the stationary wavelet transform (SWT).

This property is useful for several applications such as breakdown points detection.

The main application of the SWT is de-noising. For more information on the rationale, see [CoiD95] in References. For examples, see One-Dimensional Discrete Stationary Wavelet Analysis and Two-Dimensional Discrete Stationary Wavelet Analysis.

The principle is to average several de-noised signals. Each of them is obtained using the usual de-noising scheme (see De-Noising), but applied to the coefficients of an 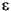-decimated DWT.

There is a restriction: we define the SWT only for signals of length divisible by 2J, where J is the maximum decomposition level, and we use the DWT with periodic extension.

Signal Extensions: Zero-Padding, Symmetrization, and Smooth Padding

-Decimated DWT

© 1994-2005 The MathWorks, Inc.