| Wavelet Toolbox | |
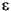-Decimated DWT
There exist a lot of slightly different ways to handle the discrete wavelet transform. Let us recall that the DWT basic computational step is a convolution followed by a decimation. The decimation retains even indexed elements.
But the decimation could be carried out by choosing odd indexed elements instead of even indexed elements. This choice concerns every step of the decomposition process, so at every level we chose odd or even.
If we perform all the different possible decompositions of the original signal, we have 2J different decompositions, for a given maximum level J.
Let us denote by 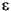j = 1 or 0 the choice of odd or even indexed elements at step j. Every decomposition is labeled by a sequence of 0's and 1's: 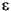= 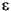1,...,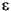J. This transform is called the 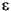-decimated DWT.
You can obtain the basis vectors of the 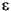-decimated DWT from those of the standard DWT by applying a shift and corresponds to a special choice of the origin of the basis functions.
| | Discrete Stationary Wavelet Transform (SWT) | How to Calculate the -Decimated DWT: SWT | |
© 1994-2005 The MathWorks, Inc.