Wavelet Toolbox

Suppressing Signals

As shown in the section Suppressing Signals, by suppressing a part of a signal the remainder may be highlighted.

Let 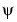be a wavelet with at least k+1 vanishing moments:

• for j = 0, ..., k,
  
  

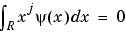
If the signal s is a polynomial of degree k, then the coefficients C(a,b) = 0 for all a and all b. Such wavelets automatically suppress the polynomials. The degree of s can vary with time x, provided that it remains less than k.

If s is now a polynomial of degree k on segment 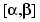, then C(a,b) = 0 as long

as the support of the function 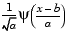is included in 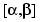. The suppression is

local. Effects will appear on the edges of the segment.

Likewise, let us suppose that, on 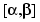to which 0 belongs, we have the

expansion 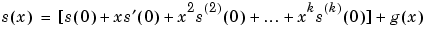. The s and g signals then have the same wavelet coefficients. This is the technical meaning of the phrase "The wavelet suppresses a polynomial part of signal s." The signal g is the "irregular" part of the signal s. The 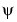wavelet systematically suppresses the regular part and analyzes the irregular part. This effect is easily seen in details D₁ through D₄ in Example 2: A Frequency Breakdown (see the curves d1, d2, d3, and d4). The wavelet suppresses the slow sine wave, which is locally assimilated to a polynomial.

Another way of suppressing a component of the signal is to modify and force certain coefficients C(a,b) to be equal to 0. Having selected a set E of indices, we stipulate that 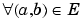, C(a,b) = 0. We then synthesize the signal using the modified coefficients.

Let us illustrate, with the following M-file, some features of wavelet processing using coefficients (resulting plots can be found in Figure 6-26).

• % Load original 1-D signal. 
  load sumsin; s = sumsin;
  
  % Set the wavelet name and perform the decomposition 
  % of s at level 4, using coif3. 
  w = 'coif3'; maxlev = 4; 
  [c,l] = wavedec(s,maxlev,w); 
  newc = c;
  
  % Force to zero the detail coefficients at levels 3 and 4. 
  newc = wthcoef('d',c,l,[3,4]);
  
  % Force the detail coefficients at level 1 to zero on 
  % original time interval [400:600] and shrink otherwise. 
  % determine first and last index of 
  % level 1 coefficients. 
  k = maxlev+1; 
  first = sum(l(1:k-1))+1; last = first+l(k)-1; 
  indd1 = first:last;
  
  % shrink by dividing by 3.
  newc(indd1) = c(indd1)/3;
  
  % find at level 1 indices of coefficients 
  % in the interval [400:600], 
  % note that time t in original grid corresponds to time 
  % t/2^k on the grid at level k. Here k=1. 
  indd1 = first+400/2:first+600/2; 
  
  % force it to zero. 
  newc(indd1) = zeros(size(indd1));
  
  % Set to 4 a coefficient at level 2 corresponding roughly 
  % to original time t = 500. 
  k = maxlev; first = sum(l(1:k-1))+1; 
  newc(first+500/2^2) = 4; 
  % Synthesize modified decomposition structure. 
  synth = waverec(newc,l,w);
  
  
  

Figure 6-26: Suppress or Modify Signal Components, Acting on Coefficients

Simple procedures to select the set of indices E are used for de-noising and compression purposes (see the sections De-Noising and Data Compression).

Wavelet Applications: More Detail

Splitting Signal Components

© 1994-2005 The MathWorks, Inc.