Wavelet Toolbox

Noise Processing

Let us first analyze noise as an ordinary signal. Then the probability characteristics correlation function, spectrum, and distribution need to be studied.

In general, for a one-dimensional discrete-time signal, the high frequencies influence the details of the first levels (the small values of j), while the low frequencies influence the deepest levels (the large values of j) and the associated approximations.

If a signal comprising only white noise is analyzed, (see for example Example 3: Uniform White Noise), the details at the various levels decrease in amplitude as the level increases. The variance of the details also decreases as the level increases. The details and approximations are not white noise anymore, as color is introduced by the filters.

On the coefficients C(j,k), where j stands for the scale and k for the time, we can add often-satisfied properties for discrete time signals:

• If the analyzed signal s is stationary, zero mean, and a white noise, the coefficients are uncorrelated.
• If furthermore s is Gaussian, the coefficients are independent and Gaussian.
• If s is a colored, stationary, zero mean Gaussian sequence, then the coefficients remain Gaussian. For each scale level j, the sequence of coefficients is a colored stationary sequence. It could be interesting to know how to choose the wavelet that would de-correlate the coefficients. This problem has not yet been resolved. Furthermore, the wavelet (if indeed it exists) most probably depends on the color of the signal. For the wavelet to be calculated, the color must be known. In most instances, this is beyond our reach.
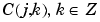• If s is a zero mean ARMA model stationary for each scale j, then is also a stationary, zero mean ARMA process whose characteristics depend on j.
• If s is a noise whose
• Correlation function is known, we know how to calculate the correlations of C(j,k) and C(j,k´).
• Spectrum is known, we know how to calculate the spectrum of C(j,k), and the cross spectrum of two different levels j and j´.

These results are easily established, since they can be deduced from the fact that the C(a,b) coefficients are calculated primarily by convolving 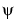and s, and using conventional formulas. The quantity that comes into play is the self-reproduction function U(a,b), which is obtained by analyzing the 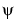wavelet as if it was a signal:

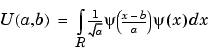
From the results for coefficients we deduce the properties of the details (and of the approximations), by using the formula

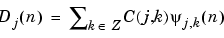
where the C(j,k) coefficients are random variables and the functions 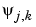are not. If the support of 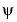is finite, only a finite number of terms will be summed.

Splitting Signal Components

De-Noising

© 1994-2005 The MathWorks, Inc.