

| Wavelet Toolbox |   |
Function Estimation: Density and Regression
In this section we present two problems of functional estimation:
Note
According to the classical statistical notations, in this section, 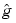 denotes the estimator of the function g instead of the Fourier transform of g. denotes the estimator of the function g instead of the Fourier transform of g.
|
Density Estimation
The data are values (X(i), 1  i
i 
n) sampled from a distribution whose density is unknown. We are looking for an estimate of this density.
The well known histogram creates the information on the density distribution of a set of measures. At the very beginning of the 19th century, Laplace, a French scientist, repeating sets of observations of the same quantity, was able to fit a simple function to the density distribution of the measures. This function is called now the Laplace-Gauss distribution.
Density estimation is a core part of reliability studies. It permits the evaluation of the life-time probability distribution of a TV set produced by a factory, the computation of the instantaneous availability, and of such other useful characteristics as the mean time to failure. A very similar situation occurs in survival analysis, when studying the residual lifetime of a medical treatment.
As in the regression context, the wavelets are useful in a nonparametric context, when very little information is available concerning the shape of the unknown density, or when you don't want to tell the statistical estimator what you know about the shape.
Several alternative competitors exist. The orthogonal basis estimators are based on the same ideas as the wavelets. Other estimators rely on statistical window techniques such as kernel smoothing methods.
We have theorems proving that the wavelet-based estimators behave at least as well as the others, and sometimes better. When the density h(x) has irregularities, such as a breakdown point or a breakdown point of the derivative h'(x), the wavelet estimator is a good solution.
How to Perform Wavelet-Based Density Estimation.
The key idea is to reduce the density estimation problem to a fixed-design regression model. More precisely the main steps are as follows:
Steps 2 through 4 are standard wavelet-based steps. But the first step of this estimation scheme depends on nb (the number of bins), which can be viewed as a bandwidth parameter. In density estimation, nb is generally small with respect to the number of observations (equal to the length of X), since the binning step is a pre-smoother. A typical default value is nb = length(X) / 4.
For more information, you can refer for example to [AntP98], [HarKPT98], and [Ogd97] in References.
Let us be a little more formal.
Let X1, X2, ... , Xn be a sequence of independent and identically distributed random variables, with a common density function 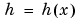 .
.
This density h is unknown and we want to estimate it. We have very little information on h.
For technical reasons we suppose that 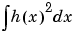 is finite. This allows us to express h in the wavelet basis.
is finite. This allows us to express h in the wavelet basis.
We know that in the basis of functions 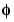 and
and 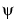 with usual notations, J being an integer,
with usual notations, J being an integer,
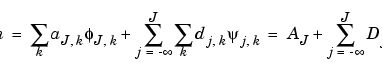
The estimator 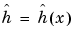 will use some wavelet coefficients. The rationale for the estimator is the following.
will use some wavelet coefficients. The rationale for the estimator is the following.
To estimate h, it is sufficient to estimate the coordinates 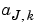 and the
and the  .
.
We know the definition of the coefficients:
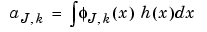
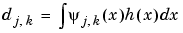
The expression of the 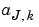 has a very funny interpretation. Because h is a density
has a very funny interpretation. Because h is a density 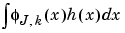 is
is 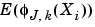 , the mean value of the random variable
, the mean value of the random variable 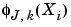 .
.
Usually such an expectation is estimated very simply by the mean value:
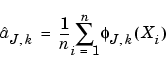
Of course the same kind of formula holds true for the 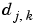 :
:
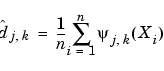
With a finite set of n observations, it is possible to estimate only a finite set of coefficients, those belonging to the levels from J-j0 up to J, and to some positions k.
Besides, several values of the 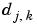 are not significant and are to be set to 0.
are not significant and are to be set to 0.
The values 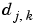 , lower than a threshold t, are set to 0 in a very similar manner as the de-noising process and for almost the same reasons.
, lower than a threshold t, are set to 0 in a very similar manner as the de-noising process and for almost the same reasons.
Inserting these expressions into the definition of h, we get an estimator:
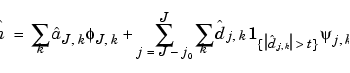
This kind of estimator avoids the oscillations that would occur if all the detail coefficients would have been kept.
From the computational viewpoint, it is difficult to use a quick algorithm because the Xi values are not equally spaced.
Note that this problem can be overcome.
Let's introduce the normalized histogram 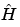 of the values of X, having nb classes, where the centers of the bins are collected in a vector Xb, the frequencies of Xi within the bins are collected in a vector Yb and then
of the values of X, having nb classes, where the centers of the bins are collected in a vector Xb, the frequencies of Xi within the bins are collected in a vector Yb and then
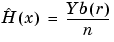 on the r-th bin
on the r-th bin
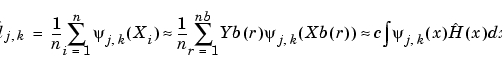
where
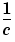 is the length of each bin.
is the length of each bin.
The signs 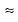 occur because we lose some information when using histogram instead of the values Xi and when approximating the integral.
occur because we lose some information when using histogram instead of the values Xi and when approximating the integral.
The last 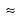 sign is very interesting. It means that
sign is very interesting. It means that 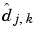 is, up to the constant c, the wavelet coefficient of the function
is, up to the constant c, the wavelet coefficient of the function 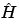 associated with the level j and the position k. The same result holds true for the
associated with the level j and the position k. The same result holds true for the 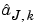 .
.
So, the last 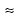 sign of the previous equation shows that the coefficients
sign of the previous equation shows that the coefficients 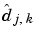 appear also to be (up to an approximation) wavelet coefficients -- those of the decomposition of the sequence
appear also to be (up to an approximation) wavelet coefficients -- those of the decomposition of the sequence 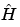 . If some of the coefficients at level J are known or computed, the Mallat algorithm computes the others quickly and simply.
. If some of the coefficients at level J are known or computed, the Mallat algorithm computes the others quickly and simply.
And now we are able to finish computing 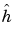 when the
when the 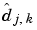 and the
and the 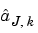 have been computed.
have been computed.
The trick is the transformation of irregularly spaced X values into equally spaced values by a process similar to the histogram computation, and that is called binning.
You can see the different steps of the procedure using the Density Estimation Graphical User Interface, by typing
and clicking the Density Estimation 1-D option.
The regression problem belongs to the family of the most common practical questions. The goal is to get a model of the relationship between one variable Y and one or more variables X. The model gives the part of the variability of Y taken in account or explained by the variation of X. A function f represents the central part of the knowledge. The remaining part is dedicated to the residuals, which are similar to a noise. The model is Y = f(X)+e.
The simplest case is the linear regression Y = aX+b+e where the function f is affine. A case a little more complicated occurs when the function belongs to a family of parametrized functions as f(X)= cos (w X), the value of w being unknown. The Statistics Toolbox provides tools for the study of such models. When f is totally unknown, the problem of the nonlinear regression is said to be a nonparametric problem and can be solved either by using usual statistical window techniques or by wavelet based methods.
These regression questions occur in many domains. For example:
Two designs are distinguished: the fixed design and the stochastic design. The difference concerns the status of X.
When the X values are chosen by the designer using a predefined scheme, as the days of the week, the age of the product, or the degree of humidity, the design is a fixed design. Usually in this case, the resulting X values are equally spaced. When X represents time, the regression problem can be viewed as a de-noising problem.
When the X values result from a measurement process or are randomly chosen, the design is stochastic. The values are often not regularly spaced. This framework is more general since it includes the analysis of the relationship between a variable Y and a general variable X, as well as the analysis of the evolution of Y as a function of time X when X is randomized.
How to Perform Wavelet-Based Regression Estimation.
The key idea is to reduce a general problem of regression to a fixed-design regression model. More precisely the main steps are as follows:
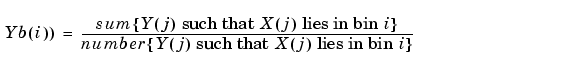
Steps 2 through 4 are standard wavelet-based steps. But the first step of this estimation scheme depends on the number of bins, which can be viewed as a bandwidth parameter. Generally, the value of nb is not chosen too small with respect to the number of observations, since the binning step is a presmoother.
For more information, you can refer for example to [AntP98], [HarKPT98], and [Ogd97]. See References.
The regression problem goes along the same lines as the density estimation. The main differences, of course, concern the model.
There is another difference with the density step: we have here two variables X and Y instead of one in the density scheme.
The regression model is 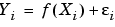 where
where 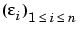 is a sequence of independent and identically distributed (i.i.d.) random variables and where the
is a sequence of independent and identically distributed (i.i.d.) random variables and where the 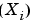 are randomly generated according to an unknown density h.
are randomly generated according to an unknown density h.
Also, let us assume that 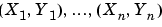 is a sequence of i.i.d. random variables.
is a sequence of i.i.d. random variables.
The function f is unknown and we look for an estimator 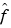 .
.
We introduce the function 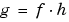 . So
. So
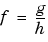 with the convention
with the convention 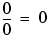 .
.
We could estimate g by a certain 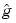 and, from the density part, an
and, from the density part, an 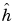 , and then use
, and then use 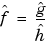 . We choose to use the estimate of h given by the histogram suitably normalized.
. We choose to use the estimate of h given by the histogram suitably normalized.
Let us bin the X-values into nb bins. The l-th bin-center is called Xb(l), the number of X-values belonging to this bin is n(l). Then, we define Yb(l) by the sum of the Y-values within the bin divided by n(l).
Let's turn to the f estimator. We shall apply the technique used for the density function. The coefficients of f, are estimated by
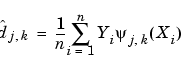

We get approximations of the coefficients by the following formula that can be written in a form proving that the approximated coefficients are also the wavelet decomposition coefficients of the sequence Yb:
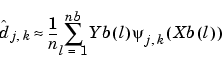
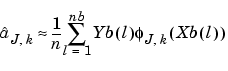
The usual simple algorithms can be used.
You can see the different steps of the procedure using the Regression Estimation Graphical User Interface by typing wavemenu, and clicking the Regression Estimation 1-D option.
 | Data Compression | Available Methods for De-Noising, Estimation, and Compression Using GUI Tools |  |
© 1994-2005 The MathWorks, Inc.