Wavelet Toolbox

Available Methods for De-Noising, Estimation, and Compression Using GUI Tools

This section presents the predefined strategies available using the de-noising, estimation, and compression GUI tools.

One-Dimensional DWT and SWT De-Noising

Level-dependent or interval-dependent thresholding methods are available. Predefined thresholding strategies:

• Hard or soft (default) thresholding
• Scaled white noise, unscaled white noise (default) or nonwhite noise
• Thresholds values are
• Donoho-Johnstone methods: Fixed-form (default), Heursure, Rigsure, Minimax
• Birgé-Massart method: Penalized high, Penalized medium, Penalized low

• The last three choices include a sparsity parameter a (a > 1).

  Using this strategy the defaults are a = 6.25, 2 and 1.5, respectively and the thresholding mode is hard. Only scaled and unscaled white noise options are supported.

One-Dimensional DWT Compression

1. Level-dependent or interval-dependent hard thresholding methods are available. Predefined thresholding strategies are
• Birgé-Massart method: Scarce high (default), Scarce medium, Scarce low

• This method includes a sparsity parameter a (1 < a < 5). Using this strategy the default is a = 1.5.

• Empirical methods

• - Equal balance sparsity-norm

  - Remove near 0

2. Global hard thresholding methods with GUI-driven choice are available. Predefined thresholding strategies are
• Empirical methods

• - Balance sparsity-norm (default = equal)

  - Remove near 0

Two-Dimensional DWT and SWT De-Noising

Level-dependent and orientation-dependent (horizontal, vertical, and diagonal) thresholding methods are available. Predefined thresholding strategies are

• Hard or soft (default) thresholding
• Scaled white noise, unscaled white noise (default) or nonwhite noise
• Thresholds values are
• Donoho-Johnstone method: Fixed form (default)
• Birgé-Massart method: Penalized high, Penalized medium, Penalized low

• The last three choices include a sparsity parameter a (a > 1). See One-Dimensional DWT and SWT De-Noising.

• Empirical method: Balance sparsity-norm, default = sqrt

Two-Dimensional DWT Compression

Level-dependent and orientation-dependent (horizontal, vertical, and diagonal) thresholding methods are available.

1. Level-dependent or interval-dependent hard thresholding methods are available. Predefined thresholding strategies are
• Birgé-Massart method: Scarce high (default); Scarce medium, Scarce low

• This method includes a sparsity parameter a (1 < a < 5), the default is a = 1.5.

• Empirical methods

• - Equal balance sparsity-norm

  - Square root of the threshold associated with Equal balance sparsity-norm

  - Remove near 0

2. Global hard thresholding methods with GUI-driven choice are available. Predefined thresholding strategies are
• Empirical methods

• - Balance sparsity-norm (default = equal); Balance sparsity-norm (sqrt)

  - Remove near 0

One-Dimensional Wavelet Packet De-Noising

Global thresholding methods with GUI-driven choice are available. Predefined thresholding strategies are

• Hard or soft (default) thresholding
• Thresholds values:
• Donoho-Johnstone methods: Fixed form (unscaled noise) (default); Fixed form (scaled noise)
• Birgé-Massart method: Penalized high, Penalized medium, Penalized low

• This method includes a sparsity parameter a (a > 1). See One-Dimensional DWT and SWT De-Noising.

One-Dimensional Wavelet Packet Compression

Global hard thresholding methods with GUI-driven choice are available. Predefined thresholding strategies are

• Empirical methods

• - Balance sparsity-norm (default = equal)

  - Remove near 0

Two-Dimensional Wavelet Packet De-Noising

Global thresholding methods with GUI-driven choice are available. Predefined thresholding strategies are

• Hard or soft (default) thresholding
• Thresholds values:
• Donoho-Johnstone methods: Fixed form (unscaled noise) (default); Fixed form (scaled noise)
• Birgé-Massart method: Penalized high, Penalized medium, Penalized low

• The last three choices include a sparsity parameter a (a > 1). See One-Dimensional DWT and SWT De-Noising.

• Empirical method: Balance sparsity-norm (sqrt)

Two-Dimensional Wavelet Packet Compression

Global thresholding methods with GUI-driven choice are available. Predefined thresholding strategies are

• Empirical methods

- Balance sparsity-norm (default = equal), Balance sparsity-norm (sqrt)

- Remove near 0

One-Dimensional Regression Estimation

A preliminary histogram estimator (binning) is used, and then the predefined thresholding strategies described in One-Dimensional DWT and SWT De-Noising are available.

Density Estimation

A preliminary histogram estimator (binning) is used, and then the predefined thresholding strategies are as follows:

• Global threshold
• By level threshold 1, By level threshold 2, By level threshold 3

The last choice includes a sparsity parameter a (a < 1); the default is 0.6.

More About the Thresholding Strategies

A lot of references are available for this topic of de-noising, estimation, and compression.

For example, [Ant94], [AntP98], [HalPKP97], [AntG99], [Ogd97], [HarKPT98], [DonJ94a&b], [DonJKP95], and [DonJKP96] (see References). A short description of the available methods previously mentioned follows.

Scarce High, Medium, and Low.   

These strategies are based on an approximation result from Birgé and Massart (for more information, see [BirM97]) and are well suited for compression.

Three parameters characterize the strategy:

• J the level of the decomposition
• M a positive constant
• a a sparsity parameter (a > 1)

The strategy is such that

• At level J the approximation is kept
• For level j from 1 to J, the n_j largest coefficients are kept with

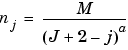
So the strategy leads to select the highest coefficients in absolute value at each level, the numbers of kept coefficients grow scarcely with J-j.

Typically, a = 1.5 for compression and a = 3 for de-noising.

A natural default value for M is the length of the coarsest approximation coefficients, since the previous formula for j = J+1, leads to M = n_J+1.

Let L denote the length of the coarsest approximation coefficients in the 1-D case and S the size of the coarsest approximation coefficients in the 2-D case.

Three different choices for M are proposed:

• Scarce high:
• M = L in the 1-D case
• M = 4*prod(S) in the 2-D case
• Scarce medium:
• M = 1.5*L in the 1-D case
• M = 4*4*prod(S) / 3 in the 2-D case
• Scarce low:
• M = 2*L in the 1-D case
• M = 4*8*prod(S) / 3 in the 2-D case

The related M-files are wdcbm, wdcbm2, and wthrmngr more information, see the corresponding reference pages).

Penalized High, Medium, and Low.   

These strategies are based on a recent de-noising result by Birgé and Massart, and can be viewed as a variant of the fixed form strategy (see the section De-Noising) of the wavelet shrinkage.

The threshold T applied to the detail coefficients for the wavelet case or the wavelet packet coefficients for a given fixed WP tree, is defined by

with

where

• The sparsity parameter a > 1
• The coefficients c(k) are sorted in decreasing order of their absolute value
• v is the noise variance

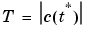
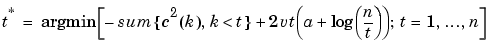
Three different intervals of choices for the sparsity parameter a are proposed:

• Penalized high, 2.5 a < 10
• Penalized medium, 1.5 < a < 2.5
• Penalized low, 1 < a < 2

The related M-files are wbmpen, wpbmpen, and wthrmngr (for more information, see the corresponding reference pages).

Remove Near 0.   

Let c denote the detail coefficients at level 1 obtained from the decomposition of the signal or the image to be compressed, using db1. The threshold value is set to median(abs(c)) or to 0.05*max(abs(c)) if median(abs(c)) = 0.

The related M-files are ddencmp and wthrmngr (for more information, see the corresponding reference pages).

Balance Sparsity-Norm.   

Let c denote all the detail coefficients; two curves are built associating, for each possible threshold value t, two percentages:

• The 2-norm recovery in percentage
• The relative sparsity in percentage, obtained from the compressed signal by setting to 0 the coefficients less than t in absolute value

A default is provided for the 1-D case taking t such that the two percentages are equal. Another one is obtained for the 2-D case by taking the square root of the previous t.

The related M-file is wthrmngr (for more information, see the corresponding reference page).

Fixed Form.   

This thresholding strategy comes from Donoho-Johnstone (see References and the 'sqtwolog' option of the wden function in De-Noising), the universal threshold is of the following form:

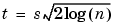• DWT or SWT 1-D, where n is the signal length and s is the noise standard deviation.
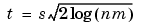• DWT or SWT 2-D, where [n,m] is the image size
• WP 1-D,
  
  
• WP 2-D,
  
  

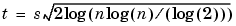
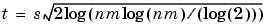
The related M-files are ddencmp, thselect, wden, wdencmp, and wthrmngr (for more information, see the corresponding reference pages).

Heursure, Rigsure, and Minimax.   

These methods are available for 1-D de-noising tools and come from Donoho-Johnstone (see References).

The related M-files are thselect, wden, wdencmp, and wthrmngr (for more information, see the corresponding reference pages).

Global, and By level 1, 2, 3.   

These options are dedicated to the density estimation problem.

See [HalPKP97], [AntG99], [Ogd97], and [HarKPT98] in References for more details.

Note that

• c is all the detail coefficients of the binned data.
• d(j) is the detail coefficients at level j.
• n is the number of bins chosen for the preliminary estimator (binning).

Then, these options are defined as follows:

1. Global:

Threshold value is set to

2. By level 1:

Level dependent thresholds T(j) are defined by

3. By level 2:

Level dependent thresholds T(j) are defined by

4. By level 3:

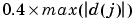
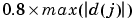
Level dependent thresholds T(j) are defined by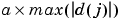

where a is a sparsity parameter (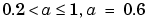 is the default)

Function Estimation: Density and Regression

Wavelet Packets

© 1994-2005 The MathWorks, Inc.