Wavelet Toolbox

Wavelet Decomposition: A Hierarchical Organization

Unlike conventional techniques, wavelet decomposition produces a family of hierarchically organized decompositions. The selection of a suitable level for the hierarchy will depend on the signal and experience. Often the level is chosen based on a desired low-pass cutoff frequency.

At each level j, we build the j-level approximation A_j, or approximation at level j, and a deviation signal called the j-level detail D_j, or detail at level j. We can consider the original signal as the approximation at level 0, denoted by A₀. The words approximation and detail are justified by the fact that A₁ is an approximation of A₀ taking into account the low frequencies of A₀, whereas the detail D₁ corresponds to the high frequency correction. Among the figures presented in the section Reconstructing Approximations and Details, one of them graphically represents this hierarchical decomposition.

One way of understanding this decomposition consists of using an optical comparison. Successive images A₁, A₂, A₃ of a given object are built. We use the same type of photographic devices, but with increasingly poor resolution. The images are successive approximations; one detail is the discrepancy between two successive images. Image A₂ is, therefore, the sum of image A₄ and intermediate details D₄, D₃:

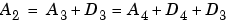
Wavelets: A New Tool for Signal Analysis

Finer and Coarser Resolutions

© 1994-2005 The MathWorks, Inc.