dbaux (Wavelet Toolbox)

Daubechies wavelet filter computation

Syntax

```
W = dbaux(N,SUMW)
W = dbaux(N)
```

Description

W = dbaux(N,SUMW) is the order N Daubechies scaling filter such that sum(W) = SUMW. Possible values for N are 1, 2, 3, ...

Note Instability may occur when N is too large.

W = dbaux(N) is equivalent to W = dbaux(N,1)

W = dbaux(N,0) is equivalent to W = dbaux(N,1)

Examples

% P the "Lagrange à trous" filter for N=2 is explicit 
% and given by: 
P = [ -1/16 0 9/16 1 9/16 0 -1/16]

P =
   -0.0625        0  0.5625  1.0000  0.5625        0 -0.0625

% The db2 Daubechies scaling filter w, is a 
% solution of the equation: P = conv(wrev(w),w) * 2.
%
% This filter P is symmetric, easy to generate, and w is 
% a minimum phase solution of the previous equation, 
% based on the roots of P. 
rP = roots(P);

% Retaining only the root inside the unit circle (here it
% is the sixth value of rP), and two roots located at -1, 
% we obtain the Daubechies wavelet of order 2:
ww = poly([rP(6) -1 -1]);    % filter construction
ww = ww / sum(ww)            % normalize sum

ww =
    0.3415  0.5915  0.1585 -0.0915

% Check that ww is correct and equal to 
% the db2 Daubechies scaling filter w. 
w = dbaux(2)

w =
    0.3415  0.5915  0.1585 -0.0915

Algorithm

The algorithm used is based on a result obtained by Shensa (see "References"), showing a correspondence between the "Lagrange à trous" filters and the convolutional squares of the Daubechies wavelet filters.

The computation of the order N Daubechies scaling filter w proceeds in two steps: compute a "Lagrange à trous" filter P, and extract a square root. More precisely:

P the associated "Lagrange à trous" filter is a symmetric filter of length
4N-1. P is defined by
P = [a(N) 0 a(N-1) 0 ... 0 a(1) 1 a(1) 0 a(2) 0 ... 0 a(N)]

where

Then, if w denotes dbN Daubechies scaling filter of sum , w is a square root of P:

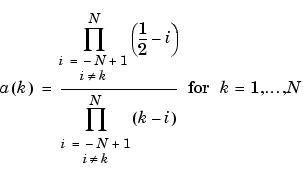
P = conv(wrev(w),w) where w is a filter of length 2N.

The corresponding polynomial has N zeros located at -1 and N-1 zeros less than 1 in modulus.

Note that other methods can be used; see various solutions of the spectral factorization problem in Strang-Nguyen (p. 157).

Limitations

The computation of the dbN Daubechies scaling filter requires the extraction of the roots of a polynomial of order 4N. Instability may occur when N is too large.

See Also
dbwavf, wfilters

References

Daubechies, I. (1992), Ten lectures on wavelets, CBMS-NSF conference series in applied mathematics, SIAM Ed.

Shensa, M.J. (1992), "The discrete wavelet transform: wedding the a trous and Mallat Algorithms," IEEE Trans. on Signal Processing, vol. 40, 10,
pp. 2464-2482.

Strang, G.; T. Nguyen (1996), Wavelets and Filter Banks, Wellesley-Cambridge Press.

cwt dbwavf