pat2cwav (Wavelet Toolbox)

Build a wavelet starting from a pattern

Syntax

[PSI,XVAL,NC] = pat2cwav(YPAT,METHOD,POLDEGREE,REGULARITY)

Description

[PSI,XVAL,NC] = pat2cwav(YPAT,METHOD,POLDEGREE,REGULARITY) computes an admissible wavelet for CWT (given by XVAL and PSI) adapted to the pattern defined by the vector YPAT, and of norm equal to 1.

The underlying x-values pattern is set to

```
xpat = linspace(0,1,length(YPAT))
```

The constant NC is such that NC*PSI approximates YPAT on the interval [0,1] by least squares fitting using

a polynomial of degree POLDEGREE when METHOD is equal to 'polynomial'
a projection on the space of functions orthogonal to constants when METHOD is equal to 'othconst'

The REGULARITY parameter defines the boundary constraints at the points 0 and 1. Allowable values are 'continuous', 'differentiable', and 'none'.

When METHOD is equal to 'polynomial'

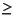if REGULARITY is equal to 'continuous', POLDEGREE must be 3
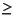if REGULARITY is equal to 'differentiable', POLDEGREE must be 5

Examples

The principle for designing a new wavelet for CWT is to approximate a given pattern using least squares optimization under constraints leading to an admissible wavelet well suited for the pattern detection using the continuous wavelet transform (see Misiti et al.).

% Example: Generate a new wavelet starting from a pattern.

% Load original pattern: a pseudo sine one.
load ptpssin1; 

% Variables X and Y contain the pattern.
whos

  Name          Size                   Bytes  Class

  IntVAL        1x1                        8  double array
  X             1x256                   2048  double array
  Y             1x256                   2048  double array
  caption       1x35                      70  char array

Grand total is 548 elements using 4174 bytes

% This example is a demo-example, so we have the value of the
% integral of the pattern as well as the details about its
% construction in the caption variable.

IntVAL

IntVAL =

    0.1592

% The pattern defined on the interval [0,1] is of integral 0.1592. 
% So it is not a wavelet but it is a good candidate since it 
% oscillates like a wavelet.
plot(X,Y), title('Original Pattern')

% To synthesize a new wavelet adapted to the given pattern, let
% us use a least squares polynomial approximation of degree 6 with
% constraints of continuity at the beginning and the end of the
% pattern.
[psi,xval,nc] = pat2cwav(Y, 'polynomial',6, 'continuous') ;

% The new wavelet is given by xval and nc*psi.
plot(X,Y,'-',xval,nc*psi,'--'), 
title('Original Pattern and Adapted Wavelet (dashed line)')

% Note that the version of the wavelet is correctly 
% defined in order to be used in the CWT algorithm must be of
% square norm equal to 1. It is simply given by xval and psi.

References

Misiti, M.; Y. Misiti, G. Oppenheim, J.-M. Poggi (2003), "Les ondelettes et leurs applications," Hermes.

orthfilt plot