wavefun (Wavelet Toolbox)

Wavelet and scaling functions

Syntax

[PHI,PSI,XVAL] = wavefun('wname',ITER)
[PHI1,PSI1,PHI2,PSI2,XVAL] = wavefun('wname',ITER)
[PSI,XVAL] = wavefun('wname',ITER)
[...] = wavefun('wname',A,B)

Description

The function wavefun returns approximations of the wavelet function 'wname' and the associated scaling function, if it exists. The positive integer ITER determines the number of iterations computed; thus, the refinement of the approximations.

For an orthogonal wavelet:

[PHI,PSI,XVAL] = wavefun('wname',ITER) returns the scaling and wavelet functions on the points grid XVAL.

For a biorthogonal wavelet:

[PHI1,PSI1,PHI2,PSI2,XVAL] = wavefun('wname',ITER) returns the scaling and wavelet functions both for decomposition (PHI1,PSI1) and for reconstruction (PHI2,PSI2).

For a Meyer wavelet:

[PHI,PSI,XVAL] = wavefun('wname',ITER)

For a wavelet without scaling function (e.g., Morlet, Mexican Hat, Gaussian derivatives wavelets or complex wavelets):

[PSI,XVAL] = wavefun('wname',ITER)

[...] = wavefun('wname',A,B), where A and B are positive integers, is equivalent to [...] = wavefun('wname',max(A,B)), and draws plots.

When A is set equal to the special value 0,

[...] = wavefun('wname',0) is equivalent to

[...] = wavefun('wname',8,0).

[...] = wavefun('wname') is equivalent to

[...] = wavefun('wname',8).

The output arguments are optional.

Examples

On the following graph, 10 piecewise linear approximations of the sym4 wavelet obtained after each iteration of the cascade algorithm are shown.

% Set number of iterations and wavelet name. 
iter = 10;
wav = 'sym4';

% Compute approximations of the wavelet function using the
% cascade algorithm. 
for i = 1:iter 
    [phi,psi,xval] = wavefun(wav,i); 
    plot(xval,psi); 
    hold on 
end
title(['Approximations of the wavelet ',wav, ... 
       ' for 1 to ',num2str(iter),' iterations']); 
hold off

Algorithm

For compactly supported wavelets defined by filters, in general no closed form analytic formula exists.

The algorithm used is the cascade algorithm. It uses the single-level inverse wavelet transform repeatedly.

Let us begin with the scaling function 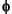phi .

Since 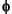phi is also equal to 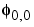, (according to the notation used in Chapter 6, "Advanced Concepts", of the User's Guide), this function is characterized by the following coefficients in the orthogonal framework:

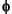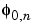< phi , > = 1 only if n = 0 and equal to 0 otherwise

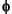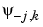< phi , > = 0 for positive j, and all k.

This expansion can be viewed as a wavelet decomposition structure. Detail coefficients are all zeros and approximation coefficients are all zeros except one equal to 1.

Then we use the reconstruction algorithm to approximate the function 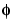over a dyadic grid, according to the following result:

For any dyadic rational of the form x = n2^-j in which the function is continuous and where j is sufficiently large, we have pointwise convergence and

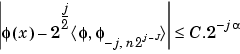
where C is a constant, and 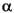alpha is a positive constant depending on the wavelet regularity.

Then using a good approximation of 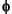phi on dyadic rationals, we can use piecewise constant or piecewise linear interpolations 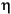eta on dyadic intervals, for which uniform convergence occurs with similar exponential rate:

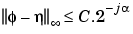
So using a J-step reconstruction scheme, we obtain an approximation that converges exponentially towards 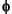phi when J goes to infinity.

Approximations are computed over a grid of dyadic rationals covering the support of the function to be approximated.

Since a scaled version of the wavelet function 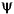psi can also be expanded on the 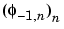, the same scheme can be used, after a single-level reconstruction

starting with the appropriate wavelet decomposition structure. Approximation coefficients are all zeros and detail coefficients are all zeros except one equal to 1.

For biorthogonal wavelets, the same ideas can be applied on each of the two multiresolution schemes in duality.

Note This algorithm may diverge if the function to be approximated is not continuous on dyadic rationals.

See Also
intwave, waveinfo, wfilters

References

Daubechies, I., Ten lectures on wavelets, CBMS, SIAM, 1992, pp. 202-213.

Strang, G.; T. Nguyen (1996), Wavelets and Filter Banks, Wellesley-Cambridge Press.

wavedemo wavefun2