Introduction to Initial Value DDE Problems :: Differential Equations (Mathematics)

Mathematics

Introduction to Initial Value DDE Problems

The DDE solver can solve systems of ordinary differential equations

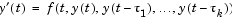
where 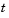is the independent variable, 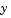is the dependent variable, and 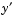y prime represents 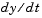d y / d t (derivative of y with respect to t) . The delays (lags) 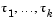tau sub 1 through tau sub n are positive constants.

Using a History to Specify the Solution of Interest

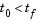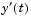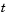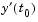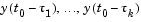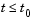In an initial value problem, we seek the solution on an interval [t sub 0, t sub f] . with t sub 0 < t sub f . The DDE shows that y prime (t) depends on values of the solution at times prior to . In particular, y prime (t sub 0) depends on y( t sub 0 minus tau sub 1) through y(t sub 0 minus tau sub k) . Because of this, a solution on depends on its values for t less than or equal t sub 0 , i.e., its history S(t) .

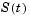Propagation of Discontinuities

Generally, the solution 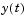y(t) of an IVP for a system of DDEs has a jump in its first derivative at the initial point 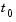t sub 0 because the first derivative of the history function does not satisfy the DDE there.

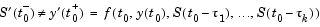
A discontinuity in any derivative propagates into the future at spacings of 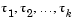tau sub 1, tau sub 2, ..., tau sub k .

For reliable and efficient integration of DDEs, a solver must track discontinuities in low order derivatives and deal with them. For DDEs with constant lags, the solution gets smoother as the integration progresses, so after a while the solver can stop tracking a discontinuity. See Discontinuities for more information.

DDE Function Summary DDE Solver