

| Mathematics |   |
DDE Solver
dde23
The DDE Solver
The function dde23 solves initial value problems for delay differential equations (DDEs) with constant delays. It integrates a system of first-order differential equations
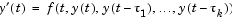
on the interval ![[t sub 0, t sub f]](diffeq30b.gif) , with
, with 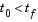 and given history
and given history 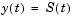 for
for 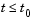 .
.
dde23 produces a solution that is continuous on ![[t sub 0, t sub f]](diffeq316a.gif) . You can use the function
. You can use the function deval and the output of dde23 to evaluate the solution at specific points on the interval of integration.
dde23 tracks discontinuities and integrates the differential equations with the explicit Runge-Kutta (2,3) pair and interpolant used by ode23. The Runge-Kutta formulas are implicit for step sizes longer than the delays. When the solution is smooth enough that steps this big are justified, the implicit formulas are evaluated by a predictor-corrector iteration.
DDE Solver Basic Syntax
The basic syntax of the DDE solver is
ddefun |
Handle to a function that evaluates the right side of the differential equations. The function must have the form where the scalar |
lags |
A vector of constant positive delays 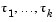 . . |
history |
Handle to a function of 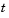 that evaluates the solution that evaluates the solution 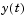 for for 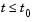 . The function must be of the form . The function must be of the form where S is a column vector. Alternatively, if history as this constant vector. If the current call to dde23 continues a previous integration to t0, use the solution sol from that call as the history. |
tspan |
The interval of integration as a two-element vector [t0,tf] with t0 < tf. |
For more advanced applications, you can specify solver options by passing an input argument options.
|
Structure of optional parameters that change the default integration properties. You can create the structure options using odeset. The odeset reference page describes the properties you can specify. |
The output argument sol is a structure created by the solver. It has fields:
sol.x |
Nodes of the mesh selected by dde23 |
sol.y |
Approximation to 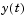 at the mesh points of at the mesh points of sol.x |
sol.yp |
Approximation to 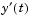 at the mesh points of at the mesh points of sol.x |
sol.solver |
'dde23' |
To evaluate the numerical solution at any point from [t0,tf], use deval with the output structure sol as its input.
 | Introduction to Initial Value DDE Problems | Solving DDE Problems |  |
© 1994-2005 The MathWorks, Inc.