Mathematics

Discontinuities

dde23 can solve problems with discontinuities in the history or discontinuities in coefficients of the equations. It provides properties that enable you to supply locations of known discontinuities and a different initial value.

Discontinuity	Property	Comments
At the initial value	InitialY	Generally the initial value is the value returned by the history function, which is to say that the solution is continuous at the initial point. However, if this is not the case, supply a different initial value using the InitialY property.
In the history, i.e., the solution at , or in the equation coefficients for t sub 0 -->	Jumps	Provide the known locations of the discontinuities in a vector as the value of the Jumps property.
State-dependent	Events	dde23 uses the events function you supply to locate these discontinuities. When dde23 finds such a discontinuity, restart the integration to continue. Specify the solution structure for the current integration as the history for the new integration. dde23 extends each element of the solution structure after each restart so that the final structure provides the solution for the whole interval of integration. If the new problem involves a change in the solution, use the InitialY property to specify the initial value for the new integration.

Example: Cardiovascular Model

This example solves a cardiovascular model due to J. T. Ottesen [6]. The equations are integrated over the interval [0,1000]. The situation of interest is when the peripheral pressure 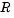is reduced exponentially from its value of 1.05 to 0.84 beginning at 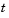= 600.

This is a problem with one delay, a constant history, and three differential equations with fourteen physical parameters. It has a discontinuity in a low order derivative at t = 600.

Note    The demo ddex2 contains the complete code for this example. To see the code in an editor, click the example name, or type edit ddex2 at the command line. To run the example type ddex2 at the command line. See DDE Solver Basic Syntax for more information.

In ddex2, the fourteen physical parameters are set as fields in a structure p that is shared with nested functions. The function ddex2de for evaluating the equations begins with

• function dydt = ddex2de(t,y,Z)
  if t <= 600
     p.R = 1.05;
  else
     p.R = 0.21 * exp(600-t) + 0.84;
  end
  .
  .
  .
  

Solve Using the Jumps Property.   The peripheral pressure 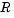is a continuous function of 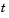, but it does not have a continuous derivative at t = 600. The example uses the Jumps property to inform dde23 about the location of this discontinuity.

• opts = ddeset('Jumps',600);
  

After defining the delay tau and the constant history, the call is

• sol = dde23(@ddex2de,tau,history,[0, 1000],opts);
  

The demo ddex2 plots only the third component, the heart rate, which shows a sharp change at t = 600.

Solve by Restarting.   The example could have solved this problem by breaking it into two pieces

• sol = dde23(@ddex2de,tau,history,[0, 600]);
  sol = dde23(@ddex2de,tau,sol,[600, 1000]);
  

The solution structure sol on the interval [0,600] serves as history for restarting the integration at t = 600. In the second call, dde23 extends sol so that on return the solution is available on the whole interval [0,1000]. That is, after this second return,

• Sint = deval(sol,[300,900]);
  

evaluates the solution obtained in the first integration at t = 300, and the solution obtained in the second integration at t = 900.

When discontinuities occur in low order derivatives at points known in advance, it is better to use the Jumps property. When you use event functions to locate such discontinuities, you must restart the integration at discontinuities.

Solving DDE Problems

Changing DDE Integration Properties

© 1994-2005 The MathWorks, Inc.