Solving DDE Problems :: Differential Equations (Mathematics)

Mathematics

Solving DDE Problems

This section uses an example to describe:

Using dde23 to solve initial value problems (IVPs) for delay differential equations (DDEs)
Evaluating the solution at specific points

Example: A Straightforward Problem

This example illustrates the straightforward formulation, computation, and display of the solution of a system of DDEs with constant delays. The history is constant, which is often the case. The differential equations are

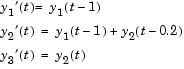
The example solves the equations on [0,5] with history

for t less than or equal 0 .

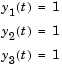
Note The demo ddex1 contains the complete code for this example. To see the code in an editor, click the example name, or type edit ddex1 at the command line. To run the example type ddex1 at the command line. See DDE Solver Basic Syntax for more information.

Rewrite the problem as a first-order system. To use dde23, you must rewrite the equations as an equivalent system of first-order differential equations. Do this just as you would when solving IVPs and BVPs for ODEs (see Examples: Solving Explicit ODE Problems). However, this example needs no such preparation because it already has the form of a first-order system of equations.
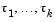Identify the lags. The delays (lags) are supplied to dde23 as a vector. For the example we could use

```
lags = [1,0.2];
```

In coding the differential equations, = lags(j).

Code the system of first-order DDEs. Once you represent the equations as a first-order system, and specify lags, you can code the equations as a function that dde23 can use.

This code represents the system in the function, ddex1de.

function dydt = ddex1de(t,y,Z)
ylag1 = Z(:,1);
ylag2 = Z(:,2);
dydt = [ylag1(1)
        ylag1(1) + ylag2(2)
        y(2)               ];

Code the history function. The history function for this example is

function S = ddex1hist(t)
S = ones(3,1);

Apply the DDE solver. The example now calls dde23 with the functions ddex1de and ddex1hist.

sol = dde23(@ddex1de,lags,@ddex1hist,[0,5]);

Here the example supplies the interval of integration [0,5] directly. Because the history is constant, we could also call dde23 by
- ```
sol = dde23(@ddex1de,lags,ones(3,1),[0,5]);
```

View the results. Complete the example by displaying the results. dde23 returns the mesh it selects and the solution there as fields in the solution structure sol. Often, these provide a smooth graph.

plot(sol.x,sol.y);
title('An example of Wille'' and Baker');
xlabel('time t');
ylabel('solution y');
legend('y_1','y_2','y_3',2)

Evaluating the Solution at Specific Points

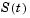The method implemented in dde23 produces a continuous solution over the whole interval of integration [t sub 0, t sub f] . You can evaluate the approximate solution, S(t) , at any point in using the helper function deval and the structure sol returned by dde23.

```
Sint = deval(sol,tint)
```

The deval function is vectorized. For a vector tint, the ith column of Sint approximates the solution 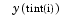y(tint(i)) .

Using the output sol from the previous example, this code evaluates the numerical solution at 100 equally spaced points in the interval [0,5] and plots the result.

tint = linspace(0,5);
Sint = deval(sol,tint);
plot(tint,Sint);

DDE Solver Discontinuities