Mathematics

Introduction to Boundary Value ODE Problems

The BVP solver is designed to handle systems of ordinary differential equations

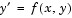
where 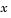is the independent variable, 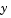is the dependent variable, and 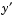represents .

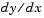See What Is an Ordinary Differential Equation? for general information about ODEs.

Using Boundary Conditions to Specify the Solution of Interest

In a boundary value problem, the solution of interest satisfies certain boundary conditions. These conditions specify a relationship between the values of the solution at more than one 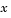. In its basic syntax, bvp4c is designed to solve two-point BVPs, i.e., problems where the solution sought on an interval must satisfy the boundary conditions

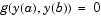
Unlike initial value problems, a boundary value problem may not have a solution, may have a finite number of solutions, or may have infinitely many solutions. As an integral part of the process of solving a BVP, you need to provide a guess for the required solution. The quality of this guess can be critical for the solver performance and even for a successful computation.

There may be other difficulties when solving BVPs, such as problems imposed on infinite intervals or problems that involve singular coefficients. Often BVPs involve unknown parameters 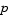that have to be determined as part of solving the problem

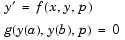
In this case, the boundary conditions must suffice to determine the value of .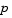

BVP Function Summary

Boundary Value Problem Solver

© 1994-2005 The MathWorks, Inc.