Introduction to Initial Value ODE Problems :: Differential Equations (Mathematics)

Mathematics

Introduction to Initial Value ODE Problems

What Is an Ordinary Differential Equation?

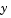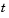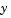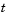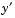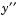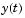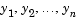The ODE solvers are designed to handle ordinary differential equations. An ordinary differential equation contains one or more derivatives of a dependent variable with respect to a single independent variable , usually referred to as time. The derivative of with respect to is denoted as y prime , the second derivative as y double prime , and so on. Often y(t) is a vector, having elements y sub 1, y sub 2 , ..., y sub n .

Types of Problems Handled by the ODE Solvers

The ODE solvers handle the following types of first-order ODEs:

Explicit ODEs of the form
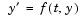
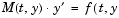Linearly implicit ODEs of the form , where M(t,y) is a matrix
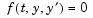Fully implicit ODEs of the form (ode15i only)

Using Initial Conditions to Specify the Solution of Interest

Generally there are many functions 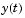y(t) that satisfy a given ODE, and additional information is necessary to specify the solution of interest. In an initial value problem, the solution of interest satisfies a specific initial condition, that is, 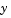is equal to 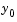y sub 0 at a given initial time 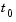t sub 0 . An initial value problem for an ODE is then

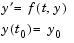
Equation 1: y prime = f(t,y).Equation 2: y(t sub 0) = y sub 0. (5-1)

If the function 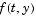f(t,y) is sufficiently smooth, this problem has one and only one solution. Generally there is no analytic expression for the solution, so it is necessary to approximate 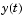y(t) by numerical means, such as using one of the ODE solvers.

Working with Higher Order ODEs

The ODE solvers accept only first-order differential equations. However, ODEs often involve a number of dependent variables, as well as derivatives of order higher than one. To use the ODE solvers, you must rewrite such equations as an equivalent system of first-order differential equations of the form

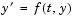
You can write any ordinary differential equation

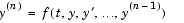
as a system of first-order equations by making the substitutions

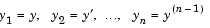
The result is an equivalent system of 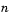first-order ODEs.

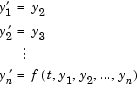
Example: Solving an IVP ODE (van der Pol Equation, Nonstiff) rewrites the second-order van der Pol equation

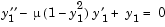
as a system of first-order ODEs.

ODE Function Summary Solvers for Explicit and Linearly Implicit ODEs