

| Mathematics |   |
Boundary Value Problem Solver
bvp4c
The BVP Solver
The function bvp4c solves two-point boundary value problems for ordinary differential equations (ODEs). It integrates a system of first-order ordinary differential equations
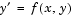
on the interval ![[a,b]](diffeq131b.gif) , subject to general two-point boundary conditions
, subject to general two-point boundary conditions
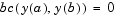
It can also accommodate other types of BVP problems, such as those that have any of the following:
In this case, the number of boundary conditions must be sufficient to determine the solution and the unknown parameters. For more information, see Finding Unknown Parameters.
bvp4c produces a solution that is continuous on ![[a,b]](diffeq131.gif) and has a continuous first derivative there. You can use the function
and has a continuous first derivative there. You can use the function deval and the output of bvp4c to evaluate the solution at specific points on the interval of integration.
bvp4c is a finite difference code that implements the 3-stage Lobatto IIIa formula. This is a collocation formula and the collocation polynomial provides a C1-continuous solution that is fourth-order accurate uniformly in the interval of integration. Mesh selection and error control are based on the residual of the continuous solution.
The collocation technique uses a mesh of points to divide the interval of integration into subintervals. The solver determines a numerical solution by solving a global system of algebraic equations resulting from the boundary conditions, and the collocation conditions imposed on all the subintervals. The solver then estimates the error of the numerical solution on each subinterval. If the solution does not satisfy the tolerance criteria, the solver adapts the mesh and repeats the process. The user must provide the points of the initial mesh as well as an initial approximation of the solution at the mesh points.
BVP Solver Basic Syntax
The basic syntax of the BVP solver is
odefun |
Handle to a function that evaluates the differential equations. It has the basic form where x is a scalar, and dydx and y are column vectors. See Function Handles in the MATLAB Programming documentation for more information. odefun can also accept a vector of unknown parameters and a variable number of known parameters. | |
bcfun |
Handle to a function that evaluates the residual in the boundary conditions. It has the basic form where ya and yb are column vectors representing y(a) and y(b), and res is a column vector of the residual in satisfying the boundary conditions. bcfun can also accept a vector of unknown parameters and a variable number of known parameters. | |
solinit |
Structure with fields x and y: | |
|
x |
Ordered nodes of the initial mesh. Boundary conditions are imposed at a = solinit.x(1) and b = solinit.x(end). |
|
y |
Initial guess for the solution with solinit.y(:,i) a guess for the solution at the node solinit.x(i). |
|
The structure can have any name, but the fields must be named x and y. It can also contain a vector that provides an initial guess for unknown parameters. You can form solinit with the helper function bvpinit. See the bvpinit reference page for details. | |
The output argument sol is a structure created by the solver. In the basic case the structure has fields x, y, yp, and solver.
sol.x |
Nodes of the mesh selected by bvp4c |
sol.y |
Approximation to 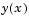 at the mesh points of at the mesh points of sol.x |
sol.yp |
Approximation to 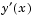 at the mesh points of at the mesh points of sol.x |
sol.solver |
'bvp4c' |
The structure sol returned by bvp4c contains an additional field if the problem involves unknown parameters:
sol.parameters |
Value of unknown parameters, if present, found by the solver. |
The function deval uses the output structure sol to evaluate the numerical solution at any point from [a,b]. For information about using deval, see Evaluating the Solution at Specific Points.
BVP Solver Options
For more advanced applications, you can specify solver options by passing an input argument options.
options |
Structure of optional parameters that change the default integration properties. This is the fourth input argument. You can create the structure options using the function bvpset. The bvpset reference page describes the properties you can specify. |
 | Introduction to Boundary Value ODE Problems | Solving BVP Problems |  |
© 1994-2005 The MathWorks, Inc.