

| Mathematics |   |
Solvers for Explicit and Linearly Implicit ODEs
This section describes the ODE solver functions for explicit or linearly implicit ODEs, as described in Types of Problems Handled by the ODE Solvers. The solver functions implement numerical integration methods for solving initial value problems for ODEs. Beginning at the initial time with initial conditions, they step through the time interval, computing a solution at each time step. If the solution for a time step satisfies the solver's error tolerance criteria, it is a successful step. Otherwise, it is a failed attempt; the solver shrinks the step size and tries again.
Mass Matrix and DAE Properties, in the reference page for odeset, explains how to set options to solve more general linearly implicit problems.
The function ode15i, which solves implicit ODEs, is described in Solver for Fully Implicit ODEs.
Solvers for Nonstiff Problems
There are three solvers designed for nonstiff problems:
ode45 |
Based on an explicit Runge-Kutta (4,5) formula, the Dormand-Prince pair. It is a one-step solver - in computing 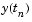 , it needs only the solution at the immediately preceding time point, , it needs only the solution at the immediately preceding time point, 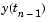 . In general, . In general, ode45 is the best function to apply as a "first try" for most problems. |
ode23 |
Based on an explicit Runge-Kutta (2,3) pair of Bogacki and Shampine. It may be more efficient than ode45 at crude tolerances and in the presence of mild stiffness. Like ode45, ode23 is a one-step solver. |
ode113 |
Variable order Adams-Bashforth-Moulton PECE solver. It may be more efficient than ode45 at stringent tolerances and when the ODE function is particularly expensive to evaluate. ode113 is a multistep solver - it normally needs the solutions at several preceding time points to compute the current solution. |
Solvers for Stiff Problems
Not all difficult problems are stiff, but all stiff problems are difficult for solvers not specifically designed for them. Solvers for stiff problems can be used exactly like the other solvers. However, you can often significantly improve the efficiency of these solvers by providing them with additional information about the problem. (See Changing ODE Integration Properties.)
There are four solvers designed for stiff problems:
ode15s |
Variable-order solver based on the numerical differentiation formulas (NDFs). Optionally it uses the backward differentiation formulas, BDFs, (also known as Gear's method). Like ode113, ode15s is a multistep solver. If you suspect that a problem is stiff or if ode45 failed or was very inefficient, try ode15s. |
ode23s |
Based on a modified Rosenbrock formula of order 2. Because it is a one-step solver, it may be more efficient than ode15s at crude tolerances. It can solve some kinds of stiff problems for which ode15s is not effective. |
ode23t |
An implementation of the trapezoidal rule using a "free" interpolant. Use this solver if the problem is only moderately stiff and you need a solution without numerical damping. |
ode23tb |
An implementation of TR-BDF2, an implicit Runge-Kutta formula with a first stage that is a trapezoidal rule step and a second stage that is a backward differentiation formula of order 2. Like ode23s, this solver may be more efficient than ode15s at crude tolerances. |
Basic ODE Solver Syntax
All of the ODE solver functions, except for ode15i, share a syntax that makes it easy to try any of the different numerical methods, if it is not apparent which is the most appropriate. To apply a different method to the same problem, simply change the ODE solver function name. The simplest syntax, common to all the solver functions, is
where solver is one of the ODE solver functions listed previously.
odefun |
Handle to a function that evaluates the system of ODEs. The function has the form where t is a scalar, and dydt and y are column vectors. See Function Handles in the MATLAB Programming documentation for more information. |
tspan |
Vector specifying the interval of integration. The solver imposes the initial conditions at tspan(1), and integrates from tspan(1) to tspan(end). |
y0 |
Vector of initial conditions for the problem See also Introduction to Initial Value ODE Problems. |
|
Structure of optional parameters that change the default integration properties. Changing ODE Integration Properties tells you how to create the structure and describes the properties you can specify. |
t |
Column vector of time points |
y |
Solution array. Each row in y corresponds to the solution at a time returned in the corresponding row of t. |
See the reference page for the ODE solvers for more information about these arguments.
 | Introduction to Initial Value ODE Problems | Examples: Solving Explicit ODE Problems |  |
© 1994-2005 The MathWorks, Inc.