Examples: Solving Explicit ODE Problems :: Differential Equations (Mathematics)

Mathematics

Examples: Solving Explicit ODE Problems

This section uses the van der Pol equation

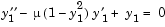
to describe the process for solving initial value ODE problems using the ODE solvers.

Example: Solving an IVP ODE (van der Pol Equation, Nonstiff) describes each step of the process. Because the van der Pol equation is a second-order equation, the example must first rewrite it as a system of first order equations.
Example: The van der Pol Equation, µ = 1000 (Stiff) demonstrates the solution of a stiff problem.
Evaluating the Solution at Specific Points tells you how to evaluate the solution at specific points.

Note See Basic ODE Solver Syntax for more information.

Example: Solving an IVP ODE (van der Pol Equation, Nonstiff)

This example explains and illustrates the steps you need to solve an initial value ODE problem:

Rewrite the problem as a system of first-order ODEs. Rewrite the van der Pol equation (second-order)

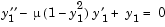
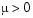where 0 --> is a scalar parameter, by making the substitution 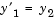. The resulting system of first-order ODEs is

See Working with Higher Order ODEs for more information.

Code the system of first-order ODEs. Once you represent the equation as a system of first-order ODEs, you can code it as a function that an ODE solver can use. The function must be of the form

```
dydt = odefun(t,y)
```

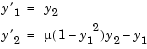
Although t and y must be the function's two arguments, the function does not need to use them. The output dydt, a column vector, is the derivative of y.

The code below represents the van der Pol system in the function, vdp1. The vdp1 function assumes that 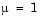. The variables 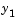and 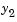are the entries y(1) and y(2) of a two-element vector.
- ```
function dydt = vdp1(t,y)
dydt = [y(2); (1-y(1)^2)*y(2)-y(1)];
```
Note that, although vdp1 must accept the arguments t and y, it does not use t in its computations.

Apply a solver to the problem. Decide which solver you want to use to solve the problem. Then call the solver and pass it the function you created to describe the first-order system of ODEs, the time interval on which you want to solve the problem, and an initial condition vector. See Examples: Solving Explicit ODE Problems and the ODE solver reference page for descriptions of the ODE solvers.

For the van der Pol system, you can use ode45 on time interval [0 20] with initial values y(1) = 2 and y(2) = 0.
- ```
[t,y] = ode45(@vdp1,[0 20],[2; 0]);
```
This example uses @ to pass vdp1 as a function handle to ode45. The resulting output is a column vector of time points t and a solution array y. Each row in y corresponds to a time returned in the corresponding row of t. The first column of y corresponds to 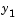, and the second column to .

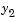Note For information on function handles, see the function_handle (@), func2str, and str2func reference pages, and the Function Handles chapter of "Programming and Data Types" in the MATLAB documentation.

View the solver output. You can simply use the plot command to view the solver output.

plot(t,y(:,1),'-',t,y(:,2),'--')
title('Solution of van der Pol Equation, \mu = 1');
xlabel('time t');
ylabel('solution y');
legend('y_1','y_2')

As an alternative, you can use a solver output function to process the output. The solver calls the function specified in the integration property OutputFcn after each successful time step. Use odeset to set OutputFcn to the desired function. See Solver Output Properties, in the reference page for odeset, for more information about OutputFcn.

Example: The van der Pol Equation, µ = 1000 (Stiff)

This example presents a stiff problem. For a stiff problem, solutions can change on a time scale that is very short compared to the interval of integration, but the solution of interest changes on a much longer time scale. Methods not designed for stiff problems are ineffective on intervals where the solution changes slowly because they use time steps small enough to resolve the fastest possible change.

When 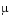is increased to 1000, the solution to the van der Pol equation changes dramatically and exhibits oscillation on a much longer time scale. Approximating the solution of the initial value problem becomes a more difficult task. Because this particular problem is stiff, a solver intended for nonstiff problems, such as ode45, is too inefficient to be practical. A solver such as ode15s is intended for such stiff problems.

The vdp1000 function evaluates the van der Pol system from the previous example, but with 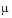= 1000.

function dydt = vdp1000(t,y)
dydt = [y(2); 1000*(1-y(1)^2)*y(2)-y(1)];

Note This example hardcodes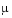

in the ODE function. The vdpode example solves the same problem, but passes a user-specified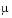

as an additional argument to the ODE function.

Now use the ode15s function to solve the problem with the initial condition vector of [2; 0], but a time interval of [0 3000]. For scaling reasons, plot just the first component of y(t).

[t,y] = ode15s(@vdp1000,[0 3000],[2; 0]);
plot(t,y(:,1),'-');
title('Solution of van der Pol Equation, \mu = 1000');
xlabel('time t');
ylabel('solution y_1');

Note For detailed instructions for solving an initial value ODE problem, see Example: Solving an IVP ODE (van der Pol Equation, Nonstiff).

Parameterizing an ODE Function

The preceding sections showed how to solve the van der Pol equation for two different values of the parameter µ. In those examples, the values µ = 1 and µ=1000 are hard-coded in the ODE functions. If you are solving an ODE for several different parameter values, it might be more convenient to include the parameter in the ODE function and assign a value to the parameter each time you run the ODE solver. This section explains how to do this for the van der Pol equation.

One way to provide parameter values to the ODE function is to write an M-file that

Accepts the parameters as inputs.
Contains ODE function as a nested function, internally using the input parameters.
Calls the ODE solver.

The following code illustrates this:

function [t,y] = run_vdp(mu)
tspan = [0 max(20, 3*mu)];
y0 = [2; 0];

% Call the ODE solver ode15s.
[t,y] = ode15s(@vdp,tspan,y0);

% Plot the results.
plot(t,y(:,1),'-');
title(strcat('Solution of van der Pol Equation, \mu =',...
num2str(mu)));
xlabel('time t');
ylabel('solution y_1');
    % Define the ODE function as nested function, 
    % using the parameter mu.
    function dydt = vdp(t,y)
    dydt = [y(2); mu*(1-y(1)^2)*y(2)-y(1)];
    end
end

Because the ODE function vdp is a nested function, the value of the parameter mu is available to it.

To run the M-file for mu = 1, as in Example: Solving an IVP ODE (van der Pol Equation, Nonstiff), enter

```
[t,y] = run_vdp(1);
```

To run the code for µ = 1000, as in Example: The van der Pol Equation, µ = 1000 (Stiff), enter

```
[t,y] = run_vdp(1000);
```

See the vdpode code for a complete example based on these functions.

Evaluating the Solution at Specific Points

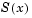The numerical methods implemented in the ODE solvers produce a continuous solution over the interval of integration [a, b] . You can evaluate the approximate solution, S(x) , at any point in [a, b] using the function deval and the structure sol returned by the solver. For example, if you solve the problem described in Example: Solving an IVP ODE (van der Pol Equation, Nonstiff) by calling ode45 with a single output argument sol,

```
sol = ode45(@vdp1,[0 20],[2; 0]);
```

ode45 returns the solution as a structure. You can then evaluate the approximate solution at points in the vector xint = 1:5 as follows:

xint = 1:5;
Sxint = deval(sol,xint)

Sxint =

    1.5081    0.3235   -1.8686   -1.7407   -0.8344
   -0.7803   -1.8320   -1.0220    0.6260    1.3095

The deval function is vectorized. For a vector xint, the ith column of Sxint approximates the solution 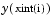y(xint(i)) .

Solvers for Explicit and Linearly Implicit ODEs Solver for Fully Implicit ODEs