

| MATLAB Function Reference |   |
Convolution and polynomial multiplication
Syntax
Description
w = conv(u,v)
convolves vectors u and v. Algebraically, convolution is the same operation as multiplying the polynomials whose coefficients are the elements of u and v.
Definition
Let m = length(u) and n = length(v). Then w is the vector of length m+n-1 whose kth element is
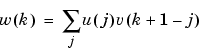
The sum is over all the values of j which lead to legal subscripts for u(j) and v(k+1-j), specifically j = max(1,k+1-n): min(k,m). When m = n, this gives
w(1) = u(1)*v(1) w(2) = u(1)*v(2)+u(2)*v(1) w(3) = u(1)*v(3)+u(2)*v(2)+u(3)*v(1) ... w(n) = u(1)*v(n)+u(2)*v(n-1)+ ... +u(n)*v(1) ... w(2*n-1) = u(n)*v(n)
Algorithm
The convolution theorem says, roughly, that convolving two sequences is the same as multiplying their Fourier transforms. In order to make this precise, it is necessary to pad the two vectors with zeros and ignore roundoff error. Thus, if
See Also
convmtx and xcorr in the Signal Processing Toolbox
 | contrast | conv2 |  |
© 1994-2005 The MathWorks, Inc.