decic (MATLAB Functions)

Compute consistent initial conditions for ode15i

Syntax

[y0mod,yp0mod] = decic(odefun,t0,y0,fixed_y0,yp0,fixed_yp0)
[y0mod,yp0mod] = decic(odefun,t0,y0,fixed_y0,yp0,fixed_yp0,options)
[y0mod,yp0mod,resnrm] = decic(...)

Description

[y0mod,yp0mod] = decic(odefun,t0,y0,fixed_y0,yp0,fixed_yp0) uses the inputs y0 and yp0 as initial guesses for an iteration to find output values that satisfy the requirement 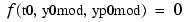, i.e., y0mod and yp0mod are consistent initial conditions. odefun is a function handle. See Function Handles in the MATLAB Programming documentation for more information. The function decic changes as few components of the guesses as possible. You can specify that decic holds certain components fixed by setting fixed_y0(i) = 1 if no change is permitted in the guess for y0(i) and 0 otherwise. decic interprets fixed_y0 = [] as allowing changes in all entries. fixed_yp0 is handled similarly.

Parameterizing Functions Called by Function Functions, in the MATLAB mathematics documentation, explains how to provide additional parameters to the function odefun, if necessary.

You cannot fix more than length(y0) components. Depending on the problem, it may not be possible to fix this many. It also may not be possible to fix certain components of y0 or yp0. It is recommended that you fix no more components than necessary.

[y0mod,yp0mod] = decic(odefun,t0,y0,fixed_y0,yp0,fixed_yp0,options) computes as above with default tolerances for consistent initial conditions, AbsTol and RelTol, replaced by the values in options, a structure you create with the odeset function.

[y0mod,yp0mod,resnrm] = decic(odefun,t0,y0,fixed_y0,yp0,fixed_yp0...) returns the norm of odefun(t0,y0mod,yp0mod) as resnrm. If the norm seems unduly large, use options to decrease RelTol (1e-3 by default).

Examples

These demos provide examples of the use of decic in solving implicit ODEs: ihb1dae, iburgersode.

See Also

ode15i, odeget, odeset, function_handle (@)

dec2hex deconv