

| MATLAB Function Reference |   |
Create or alter options structure for input to ordinary differential equation (ODE) solvers
Syntax
options = odeset('name1',value1,'name2',value2,...) options = odeset(oldopts,'name1',value1,...) options = odeset(oldopts,newopts) odeset
Description
The odeset function lets you adjust the integration parameters of the following ODE solvers.
See below for information about the integration parameters.
options = odeset('name1',value1,'name2',value2,...)
creates an options structure that you can pass as an argument to any of the ODE solvers. In the resulting structure, options, the named properties have the specified values. For example, 'name1' has the value value1. Any unspecified properties have default values. It is sufficient to type only the leading characters that uniquely identify a property name. Case is ignored for property names.
options = odeset(oldopts,'name1',value1,...)
alters an existing options structure oldopts. This sets options equal to the existing structure oldopts, overwrites any values in oldopts that are respecified using name/value pairs, and adds any new pairs to the structure. The modified structure is returned as an output argument.
options = odeset(oldopts,newopts)
alters an existing options structure oldopts by combining it with a new options structure newopts. Any new options not equal to the empty matrix overwrite corresponding options in oldopts.
odeset
with no input arguments displays all property names as well as their possible and default values.
ODE Properties
The following sections describe the properties that you can set using odeset. The available properties depend on the ODE solver you are using. There are several categories of properties:
At each step, the solver estimates the local error e in the ith component of the solution. This error must be less than or equal to the acceptable error, which is a function of the specified relative tolerance, RelTol, and the specified absolute tolerance, AbsTol.
For routine problems, the ODE solvers deliver accuracy roughly equivalent to the accuracy you request. They deliver less accuracy for problems integrated over "long" intervals and problems that are moderately unstable. Difficult problems may require tighter tolerances than the default values. For relative accuracy, adjust RelTol. For the absolute error tolerance, the scaling of the solution components is important: if |y| is somewhat smaller than AbsTol, the solver is not constrained to obtain any correct digits in y. You might have to solve a problem more than once to discover the scale of solution components.
Roughly speaking, this means that you want RelTol correct digits in all solution components except those smaller than thresholds AbsTol(i). Even if you are not interested in a component y(i) when it is small, you may have to specify AbsTol(i) small enough to get some correct digits in y(i) so that you can accurately compute more interesting components.
The following table describes the error control properties.
The following table lists the solver output properties, which control the output that the solvers generate.
| Property |
Value |
Description |
|
| OutputFcn |
Function handle {@odeplot} |
The output function is a function that the solver calls after every successful integration step. To specify an output function, set 'OutputFcn' to a function handle. For example, sets 'OutputFcn' to @myfun, a handle to the function myfun. See Function Handles in the MATLAB Programming documentation for more information.The output function must be of the form Parameterizing Functions Called by Function Functions, in the MATLAB Mathematics documentation, explains how to provide additional parameters to myfun, if necessary. |
|
The solver calls the specified output function with the following flags. Note that the syntax of the call differs with the flag. The function must respond appropriately:init -- The solver calls myfun(tspan,y0,'init') before beginning the integration to allow the output function to initialize. tspan and y0 are the input arguments to the ODE solver.{ []} -- The solver calls status = myfun(t,y,[]) after each integration step on which output is requested. t contains points where output was generated during the step, and y is the numerical solution at the points in t. If t is a vector, the ith column of y corresponds to the ith element of t.When length(tspan) > 2 the output is produced at every point in tspan. When length(tspan) = 2 the output is produced according to the Refine option.myfun must return a status output value of 0 or 1. If status = 1, the solver halts integration. You can use this mechanism, for instance, to implement a Stop button. done -- The solver calls myfun([],[],'done') when integration is complete to allow the output function to perform any cleanup chores. |
|||
You can use these general purpose output functions or you can edit them to create your own. Type help function at the command line for more information. |
|||
| OutputSel |
Vector of indices |
Vector of indices specifying which components of the solution vector are to be passed to the output function. For example, if you want to use the odeplot output function, but you want to plot only the first and third components of the solution, you can do this usingBy default, the solver passes all components of the solution to the output function. |
|
| Refine |
Positive integer |
Increases the number of output points by a factor of Refine. If Refine is 1, the solver returns solutions only at the end of each time step. If Refine is n >1, the solver subdivides each time step into n smaller intervals and returns solutions at each time point. Refine does not apply when length(tspan)>2.
Refine are computed by means of continuous extension formulas. These are specialized formulas used by the ODE solvers to obtain accurate solutions between computed time steps without significant increase in computation time. |
|
Stats |
on | {off} |
Specifies whether the solver should display statistics about its computations. By default, Stats is off. If it is on, after solving the problem the solver displays
ode23s, ode23t, ode23t, ode15s, and ode15i, also display |
The step-size properties specify the size of the first step the solver tries, potentially helping it to better recognize the scale of the problem. In addition, you can specify bounds on the sizes of subsequent time steps.
The following table describes the step-size properties.
| Property |
Value |
Description |
InitialStep |
Positive scalar |
Suggested initial step size. InitialStep sets an upper bound on the magnitude of the first step size the solver tries. If you do not set InitialStep, the initial step size is based on the slope of the solution at the initial time tspan(1), and if the slope of all solution components is zero, the procedure might try a step size that is much too large. If you know this is happening or you want to be sure that the solver resolves important behavior at the start of the integration, help the code start by providing a suitable InitialStep. |
MaxStep |
Positive scalar {0.1*abs(t0-tf)} |
Upper bound on solver step size. If the differential equation has periodic coefficients or solutions, it might be a good idea to set MaxStep to some fraction (such as 1/4) of the period. This guarantees that the solver does not enlarge the time step too much and step over a period of interest. Do not reduce MaxStep for any of the following purposes:
|
|
In some ODE problems the times of specific events are important, such as the time at which a ball hits the ground, or the time at which a spaceship returns to the earth. While solving a problem, the ODE solvers can detect such events by locating transitions to, from, or through zeros of user-defined functions.
The following table describes the Events property.
| String |
Value |
Description |
Events |
Function handle |
Handle to a function that includes one or more event functions. The function is of the formvalue, isterminal, and direction are vectors for which the ith element corresponds to the ith event function:
the solver returns these outputs as TE, YE, and IE respectively. If you call the solver as the solver returns these outputs as For examples that use an event function, see Example: Simple Event Location and Example: Advanced Event Location in the MATLAB Mathematics documentation. |
The stiff ODE solvers often execute faster if you provide additional information about the Jacobian matrix 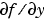 , a matrix of partial derivatives of the function that defines the differential equations.
, a matrix of partial derivatives of the function that defines the differential equations.
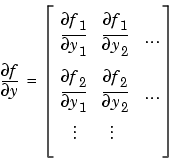
The Jacobian matrix properties pertain only to those solvers for stiff problems (ode15s, ode23s, ode23t, ode23tb, and ode15i) for which the Jacobian matrix 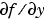 can be critical to reliability and efficiency. If you do not provide a function to calculate the Jacobian, these solvers approximate the Jacobian numerically using finite differences. In this case, you might want to use the
can be critical to reliability and efficiency. If you do not provide a function to calculate the Jacobian, these solvers approximate the Jacobian numerically using finite differences. In this case, you might want to use the Vectorized or JPattern properties.
The following table describes the Jacobian matrix properties for all implicit solvers except ode15i. See Jacobian Properties for ode15i for ode15i-specific information.
| Property |
Value |
Description |
Jacobian |
Function|handle constant matrix |
Matrix or function that evaluates the Jacobian. Supplying an analytical Jacobian often increases the speed and reliability of the solution for stiff problems. Set this property to a function FJac, where FJac(t,y) computes 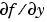 , or to the constant value of , or to the constant value of 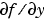 . .The Jacobian for the stiff van der Pol problem example, described in the MATLAB Mathematics documentation, can be coded as |
JPattern |
Sparse matrix of {0,1} |
Sparsity pattern with 1s where there might be nonzero entries in the Jacobian. JPattern is used to generate a sparse Jacobian matrix numerically.Set this property to a sparse matrix 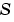 with with 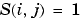 if component if component 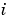 of of 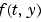 depends on component depends on component 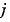 of of 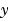 , and 0 otherwise. The solver uses this sparsity pattern to generate a sparse Jacobian matrix numerically. If the Jacobian matrix is large and sparse, this can greatly accelerate execution. For an example using the , and 0 otherwise. The solver uses this sparsity pattern to generate a sparse Jacobian matrix numerically. If the Jacobian matrix is large and sparse, this can greatly accelerate execution. For an example using the JPattern property, see Example: Large, Stiff, Sparse Problem in the MATLAB Mathematics documentation. |
Vectorized |
on | {off} |
Set on to inform the solver that you have coded the ODE function F so that F(t,[y1 y2 ...]) returns [F(t,y1) F(t,y2) ...]. This allows the solver to reduce the number of function evaluations required to compute all the columns of the Jacobian matrix, and might significantly reduce solution time.With the MATLAB array notation, it is typically an easy matter to vectorize an ODE function. For example, you can vectorize the stiff van der Pol example, described in the MATLAB Mathematics documentation, by introducing colon notation into the subscripts and by using the array power ( .^) and array multiplication (.*) operators. |
The following table describes the Jacobian matrix properties for ode15i.
Mass Matrix and DAE Properties (Solvers Other Than ode15i)
This section describes mass matrix and differential-algebraic equation (DAE) properties, which apply to all the solvers except ode15i. These properties are not applicable to ode15i and their settings do not affect its behavior.
The solvers of the ODE suite can solve ODEs of the form
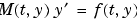
|
(2-1) |
with a mass matrix 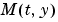 that can be sparse.
that can be sparse.
When 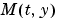 is nonsingular, the equation above is equivalent to
is nonsingular, the equation above is equivalent to 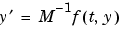 and the ODE has a solution for any initial values
and the ODE has a solution for any initial values 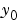 at
at 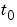 . The more general form (Equation 2-1) is convenient when you express a model naturally in terms of a mass matrix. For large, sparse
. The more general form (Equation 2-1) is convenient when you express a model naturally in terms of a mass matrix. For large, sparse 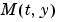 , solving Equation 2-1 directly reduces the storage and run-time needed to solve the problem.
, solving Equation 2-1 directly reduces the storage and run-time needed to solve the problem.
When 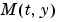 is singular, then
is singular, then 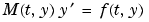 is a DAE. A DAE has a solution only when
is a DAE. A DAE has a solution only when 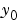 is consistent; that is, there exists an initial slope
is consistent; that is, there exists an initial slope 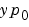 such that
such that 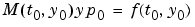 . If
. If 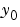 and
and 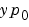 are not consistent, the solver treats them as guesses, attempts to compute consistent values that are close to the guesses, and continues to solve the problem. For DAEs of index 1, solving an initial value problem with consistent initial conditions is much like solving an ODE.
are not consistent, the solver treats them as guesses, attempts to compute consistent values that are close to the guesses, and continues to solve the problem. For DAEs of index 1, solving an initial value problem with consistent initial conditions is much like solving an ODE.
The ode15s and ode23t solvers can solve DAEs of index 1. For examples of DAE problems, see Example: Differential-Algebraic Problem, in the MATLAB Mathematics documentation, and the examples amp1dae and hb1dae.
The following table describes the mass matrix and DAE properties.
| Property |
Value |
Description |
Mass |
Matrix | function handle |
Mass matrix or a function that evaluates the mass matrix 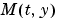 . For problems of the form . For problems of the form 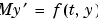 , set , set 'Mass' to a mass matrix 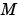 . For problems of the form . For problems of the form 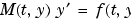 , set , set 'Mass' to a function handle @Mfun, where Mfun(t,y) evaluates the mass matrix 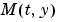 . The . The ode23s solver can only solve problems with a constant mass matrix 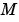 . When solving DAEs, using . When solving DAEs, using ode15s or ode23t, it is advantageous to formulate the problem so that 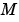 is a diagonal matrix (a semiexplicit DAE). is a diagonal matrix (a semiexplicit DAE). For example problems, see Example: Finite Element Discretization in the MATLAB Mathematics documentation, or the examples fem2ode or batonode. |
MStateDependence |
none | {weak} | strong |
Dependence of the mass matrix on 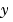 . Set this property to . Set this property to none for problems 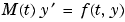 . Both . Both weak and strong indicate 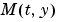 , but , but weak results in implicit solvers using approximations when solving algebraic equations. |
MvPattern |
Sparse matrix |
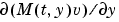 sparsity pattern. Set this property to a sparse matrix sparsity pattern. Set this property to a sparse matrix 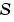 with with 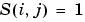 if, for any if, for any 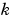 , the , the 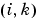 component of component of 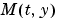 depends on component depends on component 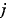 of of 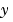 , and 0 otherwise. For use with the , and 0 otherwise. For use with the ode15s, ode23t, and ode23tb solvers when MStateDependence is strong. See burgersode as an example. |
MassSingular |
yes | no | {maybe} |
Indicates whether the mass matrix is singular. Set this property to no if the mass matrix is not singular and you are using either the ode15s or ode23t solver. The default value of maybe causes the solver to test whether the problem is a DAE, by testing whether 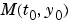 is singular. is singular. |
InitialSlope |
Vector {zero vector} |
Vector representing the consistent initial slope 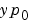 , where , where 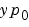 satisfies satisfies 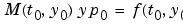 . The default is the zero vector. . The default is the zero vector. This property is for use with the ode15s and ode23t solvers when solving DAEs. |
ode15s and ode15i-Specific Properties
ode15s is a variable-order solver for stiff problems. It is based on the numerical differentiation formulas (NDFs). The NDFs are generally more efficient than the closely related family of backward differentiation formulas (BDFs), also known as Gear's methods. The ode15s properties let you choose among these formulas, as well as specifying the maximum order for the formula used.
ode15i solves fully implicit differential equations of the form
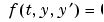
using the variable order BDF method.
The following table describes the ode15s and ode15i-specific properties. Use odeset to set these properties.
| Property |
Value |
Description |
MaxOrder |
1 | 2 | 3 | 4 | {5} |
Maximum order formula used to compute the solution. |
BDF (ode15s only) |
on | {off} |
Specifies whether you want to use the BDFs instead of the default NDFs. Set BDF on to have ode15s use the BDFs.For both the NDFs and BDFs, the formulas of orders 1 and 2 are A-stable (the stability region includes the entire left half complex plane). The higher order formulas are not as stable, and the higher the order the worse the stability. There is a class of stiff problems (stiff oscillatory) that is solved more efficiently if MaxOrder is reduced (for example to 2) so that only the most stable formulas are used. |
See Also
deval, odeget, ode45, ode23, ode23t, ode23tb, ode113, ode15s, ode23s, function_handle (@)
 | odeget | odextend |  |
© 1994-2005 The MathWorks, Inc.