

| MATLAB Function Reference |   |
Solve fully implicit differential equations, variable order method
Syntax
[T,Y] = ode15i(odefun,tspan,y0,yp0) [T,Y] = ode15i(odefun,tspan,y0,yp0,options) [T,Y,TE,YE,IE] = ode15i(...) sol = ode15i(...)
Arguments
The following table lists the input arguments for ode15i.
|
A function handle that evaluates the left side of the differential equations, which are of the form 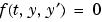 . See Function Handles in the MATLAB Programming documentation for more information. . See Function Handles in the MATLAB Programming documentation for more information. |
tspan |
A vector specifying the interval of integration, [t0,tf]. To obtain solutions at specific times (all increasing or all decreasing), use tspan = [t0,t1,...,tf]. |
y0, yp0 |
Vectors of initial conditions for 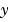 and and 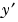 respectively. respectively. |
|
Optional integration argument created using the odeset function. See odeset for details. |
The following table lists the output arguments for ode15i.
T |
Column vector of time points |
Y |
Solution array. Each row in y corresponds to the solution at a time returned in the corresponding row of t. |
Description
[T,Y] = ode15i(odefun,tspan,y0,yp0)
with tspan = [t0 tf] integrates the system of differential equations 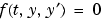 from time
from time t0 to tf with initial conditions y0 and yp0. odefun is a function handle. Function ode15i solves ODEs and DAEs of index 1. The initial conditions must be consistent, meaning that 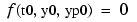 . You can use the function
. You can use the function decic to compute consistent initial conditions close to guessed values. Function odefun(t,y,yp), for a scalar t and column vectors y and yp, must return a column vector corresponding to 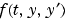 . Each row in the solution array
. Each row in the solution array Y corresponds to a time returned in the column vector T. To obtain solutions at specific times t0,t1,...,tf (all increasing or all decreasing), use tspan = [t0,t1,...,tf].
Parameterizing Functions Called by Function Functions, in the MATLAB mathematics documentation, explains how to provide additional parameters to the function odefun, if necessary.
[T,Y] = ode15i(odefun,tspan,y0,yp0,options)
solves as above with default integration parameters replaced by property values specified in options, an argument created with the odeset function. Commonly used options include a scalar relative error tolerance RelTol (1e-3 by default) and a vector of absolute error tolerances AbsTol (all components 1e-6 by default). See odeset for details.
[T,Y,TE,YE,IE] = ode15i(odefun,tspan,y0,yp0,options...)
with the 'Events' property in options set to a function events, solves as above while also finding where functions of 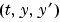 , called event functions, are zero. The function
, called event functions, are zero. The function events is of the form [value,isterminal,direction] = events(t,y,yp) and includes the necessary event functions. Code the function events so that the ith element of each output vector corresponds to the ith event. For the ith event function in events:
value(i) is the value of the function.
isterminal(i) = 1 if the integration is to terminate at a zero of this event function and 0 otherwise.
direction(i) = 0 if all zeros are to be computed (the default), +1 if only the zeros where the event function increases, and -1 if only the zeros where the event function decreases.
Output TE is a column vector of times at which events occur. Rows of YE are the corresponding solutions, and indices in vector IE specify which event occurred. See Changing ODE Integration Properties in the MATLAB documentation for more information.
sol = ode15i(odefun,[t0 tfinal],y0,yp0,...)
returns a structure that can be used with deval to evaluate the solution at any point between t0 and tf. The structure sol always includes these fields:
If you specify the Events option and events are detected, sol also includes these fields:
Options
ode15i accepts the following parameters in options. For more information, see odeset and Changing ODE Integration Properties in the MATLAB documentation.
| Error control |
RelTol, AbsTol, NormControl |
| Solver output |
OutputFcn, OutputSel, Refine, Stats |
| Event location |
Events |
| Step size |
MaxStep, InitialStep |
| Jacobian matrix |
Jacobian, JPattern, Vectorized |
Solver Output
If you specify an output function as the value of the OutputFcn property, the solver calls it with the computed solution after each time step. Four output functions are provided: odeplot, odephas2, odephas3, odeprint. When you call the solver with no output arguments, it calls the default odeplot to plot the solution as it is computed. odephas2 and odephas3 produce two- and three-dimensional phase plane plots, respectively. odeprint displays the solution components on the screen. By default, the ODE solver passes all components of the solution to the output function. You can pass only specific components by providing a vector of indices as the value of the OutputSel property. For example, if you call the solver with no output arguments and set the value of OutputSel to [1,3], the solver plots solution components 1 and 3 as they are computed.
Jacobian Matrices
The Jacobian matrices 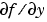 and
and 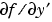 are critical to reliability and efficiency. You can provide these matrices as one of the following:
are critical to reliability and efficiency. You can provide these matrices as one of the following:
[dfdy,dfdyp] = FJAC(t,y,yp) that computes the Jacobian matrices. If FJAC returns an empty matrix [] for either dfdy or dfdyp, then ode15i approximates that matrix by finite differences.
{dfdy,dfdyp}, either of which could be empty.
Use odeset to set the Jacobian option to the function or cell array. If you do not set the Jacobian option, ode15i approximates both Jacobian matrices by finite differences.
For ode15i, Vectorized is a two-element cell array. Set the first element to 'on' if odefun(t,[y1,y2,...],yp) returns [odefun(t,y1,yp),odefun(t,y2,yp),...]. Set the second element to 'on' if odefun(t,y,[yp1,yp2,...]) returns [odefun(t,y,yp1),odefun(t,y,yp2),...]. The default value of Vectorized is {'off','off'}.
For ode15i, JPattern is also a two-element sparse matrix cell array. If 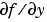 or
or 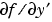 is a sparse matrix, set
is a sparse matrix, set JPattern to the sparsity patterns, {SPDY,SPDYP}. A sparsity pattern of 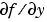 is a sparse matrix
is a sparse matrix SPDY with SPDY(i,j) = 1 if component i of f(t,y,yp) depends on component j of y, and 0 otherwise. Use SPDY = [] to indicate that 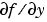 is a full matrix. Similarly for
is a full matrix. Similarly for 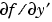 and
and SPDYP. The default value of JPattern is {[],[]}.
Examples
Example 1. This example uses a helper function decic to hold fixed the initial value for 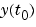 and compute a consistent initial value for
and compute a consistent initial value for 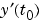 for the Weissinger implicit ODE. The Weissinger function evaluates the residual of the implicit ODE.
for the Weissinger implicit ODE. The Weissinger function evaluates the residual of the implicit ODE.
The example uses ode15i to solve the ODE, and then plots the numerical solution against the analytical solution.
Other Examples. These demos provide examples of implicit ODEs: ihb1dae, iburgersode.
See Also
decic, deval, odeget, odeset, function_handle (@)
Other ODE initial value problem solvers: ode45, ode23, ode113, ode15s, ode23s, ode23t, ode23tb
 | nzmax | ode45, ode23, ode113, ode15s, ode23s, ode23t, ode23tb |  |
© 1994-2005 The MathWorks, Inc.