| MATLAB Function Reference | |
Complete elliptic integrals of the first and second kind
Syntax
Definition
The complete elliptic integral of the first kind [1] is
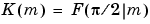
where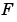 
, the elliptic integral of the first kind, is
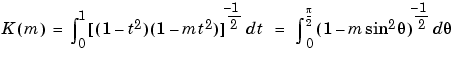
The complete elliptic integral of the second kind
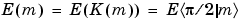
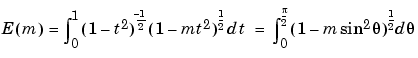
Some definitions of K and E use the modulus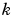 
instead of the parameter 
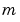. They are related by
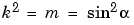
Description
K = ellipke(M)
returns the complete elliptic integral of the first kind for the elements of M.
[K,E] = ellipke(M)
returns the complete elliptic integral of the first and second kinds.
[K,E] = ellipke(M,tol)
computes the complete elliptic integral to accuracy tol. The default is eps; increase this for a less accurate but more quickly computed answer.
Algorithm
ellipke computes the complete elliptic integral using the method of the arithmetic-geometric mean described in [1], section 17.6. It starts with the triplet of numbers
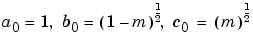
ellipke computes successive iterations of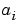 
, 
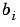, and 
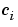with
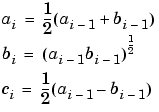
stopping at iteratio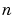n 
when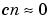 
, within the tolerance specified by eps. The complete elliptic integral of the first kind is then
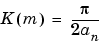
Limitations
ellipke is limited to the input domain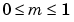 
.
See Also
References
[1] Abramowitz, M. and I.A. Stegun, Handbook of Mathematical Functions, Dover Publications, 1965, 17.6.
| | ellipj | ellipsoid | |
© 1994-2005 The MathWorks, Inc.