expm (MATLAB Functions)

Matrix exponential

Syntax

```
Y = expm(X)
```

Description

Y = expm(X) raises the constant 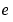to the matrix power X. The expm function produces complex results if X has nonpositive eigenvalues.

Use exp for the element-by-element exponential.

Algorithm

expm is a built-in function that uses the Padé approximation with scaling and squaring. You can see the coding of this algorithm in the expm1 demo.

Note The expmdemo1, expmdemo2, and expmdemo3 demos illustrate the use of Padé approximation, Taylor series approximation, and eigenvalues and eigenvectors, respectively, to compute the matrix exponential.

References [1] and [2] describe and compare many algorithms for computing a matrix exponential. The built-in method, expm, is essentially method 3 of [2].

Examples

This example computes and compares the matrix exponential of A and the exponential of A.

A = [1        1        0
     0        0        2
     0        0       -1 ];

expm(A) 
ans = 
    2.7183   1.7183        1.0862
    0        1.0000        1.2642
    0             0        0.3679

exp(A)
ans = 
    2.7183        2.7183        1.0000
    1.0000        1.0000        7.3891
    1.0000        1.0000        0.3679

Notice that the diagonal elements of the two results are equal. This would be true for any triangular matrix. But the off-diagonal elements, including those below the diagonal, are different.

See Also

exp, funm, logm, sqrtm

References

[1] Golub, G. H. and C. F. Van Loan, Matrix Computation, p. 384, Johns Hopkins University Press, 1983.

[2] Moler, C. B. and C. F. Van Loan, "Nineteen Dubious Ways to Compute the Exponential of a Matrix," SIAM Review 20, 1979, pp. 801-836.

expint expm1