logm (MATLAB Functions)

Matrix logarithm

Syntax

```
L = logm(A)
[L, exitflag] = logm(A)
```

Description

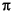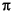L = logm(A) is the principal matrix logarithm of A, the inverse of expm(A). L is the unique logarithm for which every eigenvalue has imaginary part lying strictly between - and . If A is singular or has any eigenvalues on the negative real axis, the principal logarithm is undefined. In this case, logm computes a non-principal logarithm and returns a warning message.

[L, exitflag] = logm(A) returns a scalar exitflag that describes the exit condition of logm:

If exitflag = 0, the algorithm was successfully completed.
If exitflag = 1, one or more Taylor series evaluations did not converge. However, the computed value of L might still be accurate.

The input A can have class double or single.

Remarks

If A is real symmetric or complex Hermitian, then so is logm(A).

Some matrices, like A = [0 1; 0 0], do not have any logarithms, real or complex, so logm cannot be expected to produce one.

Limitations

For most matrices:

```
logm(expm(A)) = A = expm(logm(A))
```

These identities may fail for some A. For example, if the computed eigenvalues of A include an exact zero, then logm(A) generates infinity. Or, if the elements of A are too large, expm(A) may overflow.

Examples

Suppose A is the 3-by-3 matrix

        1        1        0
        0        0        2
        0        0       -1

and Y = expm(A) is

Y =
    2.7183    1.7183    1.0862
         0    1.0000    1.2642
         0         0    0.3679

Then A = logm(Y) produces the original matrix A.

Y =
    1.0000    1.0000    0.0000
         0         0    2.0000
         0         0   -1.0000

But log(A) involves taking the logarithm of zero, and so produces

ans =
    1.0000    0.5413    0.0826
      -Inf         0    0.2345
      -Inf      -Inf   -1.0000

Algorithm

The algorithm logm uses is described in [1].

See Also

expm, funm, sqrtm

References

[1] Davies, P. I. and N. J. Higham, "A Schur-Parlett algorithm for computing matrix functions," SIAM J. Matrix Anal. Appl., Vol. 25, Number 2, pp. 464-485, 2003.

[2] Cheng, S. H., N. J. Higham, C. S. Kenney, and A. J. Laub, "Approximating the logarithm of a matrix to specified accuracy," SIAM J. Matrix Anal. Appl., Vol. 22, Number 4, pp. 1112-1125, 2001.

[3] Higham, N. J., "Evaluating Pade approximants of the matrix logarithm," SIAM J. Matrix Anal. Appl., Vol. 22, Number 4, pp. 1126-1135, 2001.

[4] Golub, G. H. and C. F. Van Loan, Matrix Computation, Johns Hopkins University Press, 1983, p. 384.

[5] Moler, C. B. and C. F. Van Loan, "Nineteen Dubious Ways to Compute the Exponential of a Matrix," SIAM Review 20, 1979,pp. 801-836.

loglog logspace