| MATLAB Function Reference | |
Syntax
[A,B,C,...] = gallery('tmfun',P1,P2,...) gallery(3) a badly conditioned 3-by-3 matrix gallery(5) an interesting eigenvalue problem
Description
[A,B,C,...] = gallery('tmfun',P1,P2,...)
returns the test matrices specified by string tmfun. tmfun is the name of a matrix family selected from the table below. P1, P2,... are input parameters required by the individual matrix family. The number of optional parameters P1,P2,... used in the calling syntax varies from matrix to matrix.The exact calling syntaxes are detailed in the individual matrix descriptions below.
The gallery holds over fifty different test matrix functions useful for testing algorithms and other purposes.
cauchy--Cauchy matrix
C = gallery('cauchy',x,y)
returns an n-by-n matrix, C(i,j) = 1/(x(i)+y(j)). Arguments x and y are vectors of length n. If you pass in scalars for x and y, they are interpreted as vectors 1:x and 1:y.
C = gallery('cauchy',x)
returns the same as above with y = x. That is, the command returns C(i,j) = 1/(x(i)+x(j)).
Explicit formulas are known for the inverse and determinant of a Cauchy matrix. The determinant det(C) is nonzero if x and y both have distinct elements. C is totally positive if 0 < x(1) <... < x(n) and 0 < y(1) < ... < y(n).
chebspec--Chebyshev spectral differentiation matrix
C = gallery('chebspec',n,switch)
returns a Chebyshev spectral differentiation matrix of order n. Argument switch is a variable that determines the character of the output matrix. By default, switch = 0.
For switch = 0 ("no boundary conditions"), C is nilpotent (C^n = 0) and has the null vector ones(n,1). The matrix C is similar to a Jordan block of size n with eigenvalue zero.
For switch = 1, C is nonsingular and well-conditioned, and its eigenvalues have negative real parts.
The eigenvector matrix of the Chebyshev spectral differentiation matrix is ill-conditioned.
chebvand--Vandermonde-like matrix for the Chebyshev polynomials
C = gallery('chebvand',p)
produces the (primal) Chebyshev Vandermonde matrix based on the vector of points p, which define where the Chebyshev polynomial is calculated.
C = gallery('chebvand',m,p)
where m is scalar, produces a rectangular version of the above, with m rows.
If p is a vector, then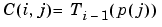 
where 
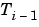is the Chebyshev polynomial of degree i-1. If p is a scalar, then p equally spaced points on the interval [0,1] are used to calculate C.
chow--Singular Toeplitz lower Hessenberg matrix
A = gallery('chow',n,alpha,delta)
returns A such that A = H(alpha) + delta*eye(n), where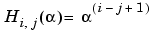 
and argument n is the order of the Chow matrix. Default value for scalars alpha and delta are 1 and 0, respectively.
H(alpha) has p = floor(n/2) eigenvalues that are equal to zero. The rest of the eigenvalues are equal to 4*alpha*cos(k*pi/(n+2))^2, k=1:n-p.
circul--Circulant matrix
C = gallery('circul',v)
returns the circulant matrix whose first row is the vector v.
A circulant matrix has the property that each row is obtained from the previous one by cyclically permuting the entries one step forward. It is a special Toeplitz matrix in which the diagonals "wrap around."
If v is a scalar, then C = gallery('circul',1:v).
The eigensystem of C (n-by-n) is known explicitly: If t is an nth root of unity, then the inner product of v and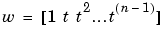 
is an eigenvalue of C and w(n:-1:1) is an eigenvector.
clement--Tridiagonal matrix with zero diagonal entries
A = gallery('clement',n,sym)
returns an n-by-n tridiagonal matrix with zeros on its main diagonal and known eigenvalues. It is singular if order n is odd. About 64 percent of the entries of the inverse are zero. The eigenvalues include plus and minus the numbers n-1, n-3, n-5, ..., as well as (for odd n) a final eigenvalue of 1 or 0.
Argument sym determines whether the Clement matrix is symmetric. For sym = 0 (the default) the matrix is nonsymmetric, while for sym = 1, it is symmetric.
compar--Comparison matrices
A = gallery('compar',A,1)
returns A with each diagonal element replaced by its absolute value, and each off-diagonal element replaced by minus the absolute value of the largest element in absolute value in its row. However, if A is triangular compar(A,1) is too.
gallery('compar',A) is diag(B) - tril(B,-1) - triu(B,1), where B = abs(A). compar(A) is often denoted by M(A) in the literature.
gallery('compar',A,0) is the same as gallery('compar',A).
condex--Counter-examples to matrix condition number estimators
A = gallery('condex',n,k,theta)
returns a "counter-example" matrix to a condition estimator. It has order n and scalar parameter theta (default 100).
The matrix, its natural size, and the estimator to which it applies are specified by k:
k = 1 |
4-by-4 |
LINPACK |
k = 2 |
3-by-3 |
LINPACK |
k = 3 |
arbitrary |
LINPACK (rcond) (independent of theta) |
k = 4 |
n >= 4 |
LAPACK (RCOND) (default). It is the inverse of this matrix that is a counter-example. |
If n is not equal to the natural size of the matrix, then the matrix is padded out with an identity matrix to order n.
cycol--Matrix whose columns repeat cyclically
A = gallery('cycol',[m n],k)
returns an m-by-n matrix with cyclically repeating columns, where one "cycle" consists of randn(m,k). Thus, the rank of matrix A cannot exceed k, and k must be a scalar.
Argument k defaults to round(n/4), and need not evenly divide n.
A = gallery('cycol',n,k),
where n is a scalar, is the same as gallery('cycol',[n n],k).
dorr--Diagonally dominant, ill-conditioned, tridiagonal matrix
[c,d,e] = gallery('dorr',n,theta)
returns the vectors defining an n-by-n, row diagonally dominant, tridiagonal matrix that is ill-conditioned for small nonnegative values of theta. The default value of theta is 0.01. The Dorr matrix itself is the same as gallery('tridiag',c,d,e).
A = gallery('dorr',n,theta)
returns the matrix itself, rather than the defining vectors.
dramadah--Matrix of zeros and ones whose inverse has large integer entries
A = gallery('dramadah',n,k)
returns an n-by-n matrix of 0's and 1's for which mu(A) = norm(inv(A),'fro') is relatively large, although not necessarily maximal. An anti-Hadamard matrix A is a matrix with elements 0 or 1 for which mu(A) is maximal.
n and k must both be scalars. Argument k determines the character of the output matrix:
fiedler--Symmetric matrix
A = gallery('fiedler',c),
where c is a length n vector, returns the n-by-n symmetric matrix with elements abs(n(i)-n(j)). For scalar c, A = gallery('fiedler',1:c).
Matrix A has a dominant positive eigenvalue and all the other eigenvalues are negative.
Explicit formulas for inv(A) and det(A) are given in [Todd, J., Basic Numerical Mathematics, Vol. 2: Numerical Algebra, Birkhauser, Basel, and Academic Press, New York, 1977, p. 159] and attributed to Fiedler. These indicate that inv(A) is tridiagonal except for nonzero (1,n) and (n,1) elements.
forsythe--Perturbed Jordan block
A = gallery('forsythe',n,alpha,lambda)
returns the n-by-n matrix equal to the Jordan block with eigenvalue lambda, excepting that A(n,1) = alpha. The default values of scalars alpha and lambda are sqrt(eps) and 0, respectively.
The characteristic polynomial of A is given by:
frank--Matrix with ill-conditioned eigenvalues
F = gallery('frank',n,k)
returns the Frank matrix of order n. It is upper Hessenberg with determinant 1. If k = 1, the elements are reflected about the anti-diagonal (1,n)--(n,1). The eigenvalues of F may be obtained in terms of the zeros of the Hermite polynomials. They are positive and occur in reciprocal pairs; thus if n is odd, 1 is an eigenvalue. F has floor(n/2) ill-conditioned eigenvalues--the smaller ones.
gearmat--Gear matrix
A = gallery('gearmat',n,i,j)
returns the n-by-n matrix with ones on the sub- and super-diagonals, sign(i) in the (1,abs(i)) position, sign(j) in the (n,n+1-abs(j)) position, and zeros everywhere else. Arguments i and j default to n and -n, respectively.
Matrix A is singular, can have double and triple eigenvalues, and can be defective.
All eigenvalues are of the form 2*cos(a) and the eigenvectors are of the form [sin(w+a), sin(w+2*a), ..., sin(w+n*a)], where a and w are given in Gear, C. W., "A Simple Set of Test Matrices for Eigenvalue Programs", Math. Comp., Vol. 23 (1969), pp. 119-125.
grcar--Toeplitz matrix with sensitive eigenvalues
A = gallery('grcar',n,k)
returns an n-by-n Toeplitz matrix with -1s on the subdiagonal, 1s on the diagonal, and k superdiagonals of 1s. The default is k = 3. The eigenvalues are sensitive.
hanowa--Matrix whose eigenvalues lie on a vertical line in the complex plane
A = gallery('hanowa',n,d)
returns an n-by-n block 2-by-2 matrix of the form:
Argument n is an even integer n=2*m. Matrix A has complex eigenvalues of the form d ± k*i, for 1 <= k <= m. The default value of d is -1.
house--Householder matrix
[v,beta,s] = gallery('house',x,k)
takes x, an n-element column vector, and returns V and beta such that H*x = s*e1. In this expression, e1 is the first column of eye(n), abs(s) = norm(x), and H = eye(n) - beta*V*V' is a Householder matrix.
k = 0 |
sign(s) = -sign(x(1)) (default) |
k = 1 |
sign(s) = sign(x(1)) |
k = 2 |
sign(s) = 1 (x must be real) |
If x is complex, then sign(x) = x./abs(x) when x is nonzero.
If x = 0, or if x = alpha*e1 (alpha >= 0) and either k = 1 or k = 2, then V = 0, beta = 1, and s = x(1). In this case, H is the identity matrix, which is not strictly a Householder matrix.
invhess--Inverse of an upper Hessenberg matrix
A = gallery('invhess',x,y),
where x is a length n vector and y is a length n-1 vector, returns the matrix whose lower triangle agrees with that of ones(n,1)*x' and whose strict upper triangle agrees with that of [1 y]*ones(1,n).
The matrix is nonsingular if x(1) ~= 0 and x(i+1) ~= y(i) for all i, and its inverse is an upper Hessenberg matrix. Argument y defaults to -x(1:n-1).
If x is a scalar, invhess(x) is the same as invhess(1:x).
invol--Involutory matrix
A = gallery('invol',n)
returns an n-by-n involutory (A*A = eye(n)) and ill-conditioned matrix. It is a diagonally scaled version of hilb(n).
B = (eye(n)-A)/2 and B = (eye(n)+A)/2 are idempotent (B*B = B).
ipjfact--Hankel matrix with factorial elements
[A,d] = gallery('ipjfact',n,k)
returns A, an n-by-n Hankel matrix, and d, the determinant of A, which is known explicitly. If k = 0 (the default), then the elements of A are A(i,j) = (i+j)! If k = 1, then the elements of A are A(i,j) = 1/(i+j).
Note that the inverse of A is also known explicitly.
jordbloc--Jordan block
A = gallery('jordbloc',n,lambda)
returns the n-by-n Jordan block with eigenvalue lambda. The default value for lambda is 1.
kahan--Upper trapezoidal matrix
A = gallery('kahan',n,theta,pert)
returns an upper trapezoidal matrix that has interesting properties regarding estimation of condition and rank.
If n is a two-element vector, then A is n(1)-by-n(2); otherwise, A is n-by-n. The useful range of theta is 0 < theta < pi, with a default value of 1.2.
To ensure that the QR factorization with column pivoting does not interchange columns in the presence of rounding errors, the diagonal is perturbed by pert*eps*diag([n:-1:1]). The default pert is 25, which ensures no interchanges for gallery('kahan',n) up to at least n = 90 in IEEE arithmetic.
kms--Kac-Murdock-Szego Toeplitz matrix
A = gallery('kms',n,rho)
returns the n-by-n Kac-Murdock-Szego Toeplitz matrix such that A(i,j) = rho^(abs(i-j)), for real rho.
For complex rho, the same formula holds except that elements below the diagonal are conjugated. rho defaults to 0.5.
The KMS matrix A has these properties:
L = inv(gallery('triw',n,-rho,1))', and D(i,i) = (1-abs(rho)^2)*eye(n), except D(1,1) = 1.
0 < abs(rho) < 1.
inv(A) is tridiagonal.
krylov--Krylov matrix
B = gallery('krylov',A,x,j)
returns the Krylov matrix
where A is an n-by-n matrix and x is a length n vector. The defaults are x = ones(n,1), and j = n.
B = gallery('krylov',n)
is the same as gallery('krylov',(randn(n)).
lauchli--Rectangular matrix
A = gallery('lauchli',n,mu)
returns the (n+1)-by-n matrix
The Lauchli matrix is a well-known example in least squares and other problems that indicates the dangers of forming A'*A. Argument mu defaults to sqrt(eps).
lehmer--Symmetric positive definite matrix
A = gallery('lehmer',n)
returns the symmetric positive definite n-by-n matrix such that A(i,j) = i/j for j >= i.
The Lehmer matrix A has these properties:
A is totally nonnegative.
inv(A) is tridiagonal and explicitly known.
n <= cond(A) <= 4*n*n.
leslie--
L = gallery('leslie',a,b)
is the n-by-n matrix from the Leslie population model with average birth numbers a(1:n) and survival rates b(1:n-1). It is zero, apart from the first row (which contains the a(i)) and the first subdiagonal (which contains the b(i)). For a valid model, the a(i) are nonnegative and the b(i) are positive and bounded by 1, i.e., 0 < b(i) <= 1.
L = gallery('leslie',n)
generates the Leslie matrix with a = ones(n,1), b = ones(n-1,1).
lesp--Tridiagonal matrix with real, sensitive eigenvalues
A = gallery('lesp',n)
returns an n-by-n matrix whose eigenvalues are real and smoothly distributed in the interval approximately [-2*N-3.5, -4.5].
The sensitivities of the eigenvalues increase exponentially as the eigenvalues grow more negative. The matrix is similar to the symmetric tridiagonal matrix with the same diagonal entries and with off-diagonal entries 1, via a similarity transformation with D = diag(1!,2!,...,n!).
lotkin--Lotkin matrix
A = gallery('lotkin',n)
returns the Hilbert matrix with its first row altered to all ones. The Lotkin matrix A is nonsymmetric, ill-conditioned, and has many negative eigenvalues of small magnitude. Its inverse has integer entries and is known explicitly.
minij--Symmetric positive definite matrix
A = gallery('minij',n)
returns the n-by-n symmetric positive definite matrix with A(i,j) = min(i,j).
The minij matrix has these properties:
inv(A) is tridiagonal and equal to -1 times the second difference matrix, except its (n,n) element is 1.
2*A-ones(size(A)), has tridiagonal inverse and eigenvalues 0.5*sec((2*r-1)*pi/(4*n))^2, where r=1:n.
(n+1)*ones(size(A))-A has elements that are max(i,j) and a tridiagonal inverse.
moler--Symmetric positive definite matrix
A = gallery('moler',n,alpha)
returns the symmetric positive definite n-by-n matrix U'*U, where U = gallery('triw',n,alpha).
For the default alpha = -1, A(i,j) = min(i,j)-2, and A(i,i) = i. One of the eigenvalues of A is small.
neumann--Singular matrix from the discrete Neumann problem (sparse)
C = gallery('neumann',n)
returns the sparse n-by-n singular, row diagonally dominant matrix resulting from discretizing the Neumann problem with the usual five-point operator on a regular mesh. Argument n is a perfect square integer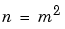 
or a two-element vector. C is sparse and has a one-dimensional null space with null vector ones(n,1).
orthog--Orthogonal and nearly orthogonal matrices
Q = gallery('orthog',n,k)
returns the kth type of matrix of order n, where k > 0 selects exactly orthogonal matrices, and k < 0 selects diagonal scalings of orthogonal matrices. Available types are:
parter--Toeplitz matrix with singular values near pi
C = gallery('parter',n)
returns the matrix C such that C(i,j) = 1/(i-j+0.5).
C is a Cauchy matrix and a Toeplitz matrix. Most of the singular values of C are very close to pi.
pei--Pei matrix
A = gallery('pei',n,alpha),
where alpha is a scalar, returns the symmetric matrix alpha*eye(n) + ones(n). The default for alpha is 1. The matrix is singular for alpha equal to either 0 or -n.
poisson--Block tridiagonal matrix from Poisson's equation (sparse)
A = gallery('poisson',n)
returns the block tridiagonal (sparse) matrix of order n^2 resulting from discretizing Poisson's equation with the 5-point operator on an n-by-n mesh.
prolate--Symmetric, ill-conditioned Toeplitz matrix
A = gallery('prolate',n,w)
returns the n-by-n prolate matrix with parameter w. It is a symmetric Toeplitz matrix.
If 0 < w < 0.5 then A is positive definite
A are distinct, lie in (0,1), and tend to cluster around 0 and 1.
w is 0.25.
randcolu -- Random matrix with normalized cols and specified singular values
A = gallery('randcolu',n)
is a random n-by-n matrix with columns of unit 2-norm, with random singular values whose squares are from a uniform distribution.
A'*A is a correlation matrix of the form produced by gallery('randcorr',n).
gallery('randcolu',x)
where x is an n-vector (n > 1), produces a random n-by-n matrix having singular values given by the vector x. The vector x must have nonnegative elements whose sum of squares is n.
gallery('randcolu',x,m)
where m >= n, produces an m-by-n matrix.
gallery('randcolu',x,m,k)
provides a further option:
[1] Davies, P. I. and N. J. Higham, "Numerically Stable Generation of Correlation Matrices and Their Factors," BIT, Vol. 40, 2000, pp. 640-651.
randcorr -- Random correlation matrix with specified eigenvalues
gallery('randcorr',n)
is a random n-by-n correlation matrix with random eigenvalues from a uniform distribution. A correlation matrix is a symmetric positive semidefinite matrix with 1s on the diagonal (see corrcoef).
gallery('randcorr',x)
produces a random correlation matrix having eigenvalues given by the vector x, where length(x) > 1. The vector x must have nonnegative elements summing to length(x).
gallery('randcorr',x,k)
provides a further option:
[1] Bendel, R. B. and M. R. Mickey, "Population Correlation Matrices for Sampling Experiments," Commun. Statist. Simulation Comput., B7, 1978, pp. 163-182.
[2] Davies, P. I. and N. J. Higham, "Numerically Stable Generation of Correlation Matrices and Their Factors," BIT, Vol. 40, 2000, pp. 640-651.
randhess--Random, orthogonal upper Hessenberg matrix
H = gallery('randhess',n)
returns an n-by-n real, random, orthogonal upper Hessenberg matrix.
H = gallery('randhess',x)
if x is an arbitrary, real, length n vector with n > 1, constructs H nonrandomly using the elements of x as parameters.
Matrix H is constructed via a product of n-1 Givens rotations.
randjorth--Random J-orthogonal matrix
A = gallery('randjorth', n), for a positive integer n, produces a random n-by-n J-orthogonal matrix A, where
J-orthogonality means that A'*J*A = J. Such matrices are sometimes called hyperbolic.
A = gallery('randjorth', n, m), for positive integers n and m, produces a random (n+m)-by-(n+m) J-orthogonal matrix A, where
A = gallery('randjorth',n,m,c,symm,method)
uses the following optional input arguments:
c -- Specifies cond(A) to be the scalar c.
symm -- Enforces symmetry if the scalar symm is nonzero.
method -- calls qr to perform the underlying orthogonal transformations if the scalar method is nonzero. A call to qr is much faster than the default method for large dimensions
rando--Random matrix composed of elements -1, 0 or 1
A = gallery('rando',n,k)
returns a random n-by-n matrix with elements from one of the following discrete distributions:
k = 1 |
A(i,j) = 0 or 1 with equal probability (default). |
k = 2 |
A(i,j) = -1 or 1 with equal probability. |
k = 3 |
A(i,j) = -1, 0 or 1 with equal probability. |
Argument n may be a two-element vector, in which case the matrix is n(1)-by-n(2).
randsvd--Random matrix with preassigned singular values
A = gallery('randsvd',n,kappa,mode,kl,ku)
returns a banded (multidiagonal) random matrix of order n with cond(A) = kappa and singular values from the distribution mode. If n is a two-element vector, A is n(1)-by-n(2).
Arguments kl and ku specify the number of lower and upper off-diagonals, respectively, in A. If they are omitted, a full matrix is produced. If only kl is present, ku defaults to kl.
Condition number kappa defaults to sqrt(1/eps). In the special case where kappa < 0, A is a random, full, symmetric, positive definite matrix with cond(A) = -kappa and eigenvalues distributed according to mode. Arguments kl and ku, if present, are ignored.
A = gallery('randsvd',n,kappa,mode,kl,ku,method)
specifies how the computations are carried out. method = 0 is the default, while method = 1 uses an alternative method that is much faster for large dimensions, even though it uses more flops.
redheff--Redheffer's matrix of 1s and 0s
A = gallery('redheff',n)
returns an n-by-n matrix of 0's and 1's defined by A(i,j) = 1, if j = 1 or if i divides j, and A(i,j) = 0 otherwise.
The Redheffer matrix has these properties:
(n-floor(log2(n)))-1 eigenvalues equal to 1
sqrt(n)
-sqrt(n)
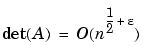for every epsilon > 0.
Barrett and Jarvis conjecture that "the small eigenvalues all lie inside the unit circle abs(Z) = 1," and a proof of this conjecture, together with a proof that some eigenvalue tends to zero as n tends to infinity, would yield a new proof of the prime number theorem.
riemann--Matrix associated with the Riemann hypothesis
A = gallery('riemann',n)
returns an n-by-n matrix for which the Riemann hypothesis is true if and only if
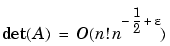
The Riemann matrix is defined by:
where B(i,j) = i-1 if i divides j, and B(i,j) = -1 otherwise.
The Riemann matrix has these properties:
. e(i) satisfies abs(e(i)) <= m-1/m, where m = n+1.
i <= e(i) <= i+1 with at most m-sqrt(m) exceptions.
(m/3, m/2] are eigenvalues.
ris--Symmetric Hankel matrix
A = gallery('ris',n)
returns a symmetric n-by-n Hankel matrix with elements
The eigenvalues of A cluster arou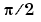nd 
and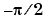 
. This matrix was invented by F.N. Ris.
smoke--Complex matrix with a 'smoke ring' pseudospectrum
A = gallery('smoke',n)
returns an n-by-n matrix with 1's on the superdiagonal, 1 in the (n,1) position, and powers of roots of unity along the diagonal.
A = gallery('smoke',n,1)
returns the same except that element A(n,1) is zero.
The eigenvalues of gallery('smoke',n,1) are the nth roots of unity; those of gallery('smoke',n) are the nth roots of unity times 2^(1/n).
toeppd--Symmetric positive definite Toeplitz matrix
A = gallery('toeppd',n,m,w,theta)
returns an n-by-n symmetric, positive semi-definite (SPD) Toeplitz matrix composed of the sum of m rank 2 (or, for certain theta, rank 1) SPD Toeplitz matrices. Specifically,
where T(theta(k)) has (i,j) element cos(2*pi*theta(k)*(i-j)).
By default: m = n, w = rand(m,1), and theta = rand(m,1).
toeppen--Pentadiagonal Toeplitz matrix (sparse)
P = gallery('toeppen',n,a,b,c,d,e)
returns the n-by-n sparse, pentadiagonal Toeplitz matrix with the diagonals: P(3,1) = a, P(2,1) = b, P(1,1) = c, P(1,2) = d, and P(1,3) = e, where a, b, c, d, and e are scalars.
By default, (a,b,c,d,e) = (1,-10,0,10,1), yielding a matrix of Rutishauser. This matrix has eigenvalues lying approximately on the line segment 2*cos(2*t) + 20*i*sin(t).
tridiag--Tridiagonal matrix (sparse)
A = gallery('tridiag',c,d,e)
returns the tridiagonal matrix with subdiagonal c, diagonal d, and superdiagonal e. Vectors c and e must have length(d)-1.
A = gallery('tridiag',n,c,d,e),
where c, d, and e are all scalars, yields the Toeplitz tridiagonal matrix of order n with subdiagonal elements c, diagonal elements d, and superdiagonal elements e. This matrix has eigenvalues
A = gallery('tridiag',n)
is the same as A = gallery('tridiag',n,-1,2,-1), which is a symmetric positive definite M-matrix (the negative of the second difference matrix).
triw--Upper triangular matrix discussed by Wilkinson and others
A = gallery('triw',n,alpha,k)
returns the upper triangular matrix with ones on the diagonal and alphas on the first k >= 0 superdiagonals.
Order n may be a 2-element vector, in which case the matrix is n(1)-by-n(2) and upper trapezoidal.
Ostrowski ["On the Spectrum of a One-parametric Family of Matrices, J. Reine Angew. Math., 1954] shows that
and, for large abs(alpha), cond(gallery('triw',n,alpha)) is approximately abs(alpha)^n*sin(pi/(4*n-2)).
Adding -2^(2-n) to the (n,1) element makes triw(n) singular, as does adding -2^(1-n) to all the elements in the first column.
vander--Vandermonde matrix
A = gallery('vander',c)
returns the Vandermonde matrix whose second to last column is c. The jth column of a Vandermonde matrix is given by A(:,j) = C^(n-j).
wathen--Finite element matrix (sparse, random entries)
A = gallery('wathen',nx,ny)
returns a sparse, random, n-by-n finite element matrix where n = 3*nx*ny + 2*nx + 2*ny + 1.
Matrix A is precisely the "consistent mass matrix" for a regular nx-by-ny grid of 8-node (serendipity) elements in two dimensions. A is symmetric, positive definite for any (positive) values of the "density," rho(nx,ny), which is chosen randomly in this routine.
A = gallery('wathen',nx,ny,1)
returns a diagonally scaled matrix such that
where D = diag(diag(A)) for any positive integers nx and ny and any densities rho(nx,ny).
wilk--Various matrices devised or discussed by Wilkinson
[A,b] = gallery('wilk',n)
returns a different matrix or linear system depending on the value of n.
n = 3 |
Upper triangular system Ux=b illustrating inaccurate solution. |
n = 4 |
Lower triangular system Lx=b, ill-conditioned. |
n = 5 |
hilb(6)(1:5,2:6)*1.8144. A symmetric positive definite matrix. |
n = 21 |
W21+, a tridiagonal matrix. Eigenvalue problem. For more detail, see [2]. |
See Also
hadamard, hilb, invhilb, magic, wilkinson
References
[1] The MATLAB gallery of test matrices is based upon the work of Nicholas J.
Higham at the Department of Mathematics, University of Manchester,
Manchester, England. Additional detail on these matrices is documented in
The Test Matrix Toolbox for MATLAB by N. J. Higham, September, 1995. This
report is available via anonymous ftp from The MathWorks at
http://www.mathworks.com/access/pub/testmatrix.ps or on the Web at
ftp://ftp.ma.man.ac.uk/pub/narep or
http://www.ma.man.ac.uk/MCCM/MCCM.html. Further background can be
found in the book Accuracy and Stability of Numerical Algorithms, Nicholas J.
Higham, SIAM, 1996.
[2] Wilkinson, J. H., The Algebraic Eigenvalue Problem, Oxford University Press, London, 1965, p.308.
| | fzero | gamma, gammainc, gammaln | |
© 1994-2005 The MathWorks, Inc.