griddatan (MATLAB Functions)

Data gridding and hypersurface fitting (dimension >= 2)

Syntax

yi = griddatan(X,y,xi)
yi = griddatan(x,y,z,v,xi,yi,zi,method)
yi = griddatan(x,y,z,v,xi,yi,zi,method,options)

Description

yi = griddatan(X, y, xi) fits a hyper-surface of the form 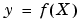to the data in the (usually) nonuniformly-spaced vectors (X, y). griddatan interpolates this hyper-surface at the points specified by xi to produce yi. xi can be nonuniform.

X is of dimension m-by-n, representing m points in n-dimensional space. y is of dimension m-by-1, representing m values of the hyper-surface 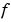(X). xi is a vector of size p-by-n, representing p points in the n-dimensional space whose surface value is to be fitted. yi is a vector of length p approximating the values 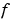(xi). The hypersurface always goes through the data points (X,y). xi is usually a uniform grid (as produced by meshgrid).

yi = griddatan(x,y,z,v,xi,yi,zi,method) defines the type of surface fit to the data, where 'method' is one of:

'linear'
Tessellation-based linear interpolation (default)

'nearest'
Nearest neighbor interpolation

`'linear'`	Tessellation-based linear interpolation (default)
`'nearest'`	Nearest neighbor interpolation

All the methods are based on a Delaunay tessellation of the data.

If method is [], the default 'linear' method is used.

yi = griddatan(x,y,z,v,xi,yi,zi,method,options) specifies a cell array of strings options to be used in Qhull via delaunayn.

If options is [], the default options are used. If options is {''}, no options are used, not even the default.

Algorithm

The griddatan methods are based on a Delaunay triangulation of the data that uses Qhull [2]. For information about Qhull, see http://www.qhull.org/. For copyright information, see http://www.qhull.org/COPYING.txt.

Reference

[1] Barber, C. B., D.P. Dobkin, and H.T. Huhdanpaa, "The Quickhull Algorithm for Convex Hulls," ACM Transactions on Mathematical Software, Vol. 22, No. 4, Dec. 1996, p. 469-483. Available in HTML format at http://www.acm.org/pubs/citations/journals/toms/1996-22-4/p469-barber.

[2] National Science and Technology Research Center for Computation and Visualization of Geometric Structures (The Geometry Center), University of Minnesota. 1993.

griddata3 gsvd