MATLAB Function Reference

interp2

Two-dimensional data interpolation (table lookup)

Syntax

• ZI = interp2(X,Y,Z,XI,YI)
  ZI = interp2(Z,XI,YI)
  ZI = interp2(Z,ntimes)
  ZI = interp2(X,Y,Z,XI,YI,method)
  ZI = interp2(...,method, extrapval)
  

Description

ZI = interp2(X,Y,Z,XI,YI) returns matrix ZI containing elements corresponding to the elements of XI and YI and determined by interpolation within the two-dimensional function specified by matrices X, Y, and Z. X and Y must be monotonic, and have the same format ("plaid") as if they were produced by meshgrid. Matrices X and Y specify the points at which the data Z is given. Out of range values are returned as NaNs.

XI and YI can be matrices, in which case interp2 returns the values of Z corresponding to the points (XI(i,j),YI(i,j)). Alternatively, you can pass in the row and column vectors xi and yi, respectively. In this case, interp2 interprets these vectors as if you issued the command meshgrid(xi,yi).

ZI = interp2(Z,XI,YI) assumes that X = 1:n and Y = 1:m, where [m,n] = size(Z).

ZI = interp2(Z,ntimes) expands Z by interleaving interpolates between every element, working recursively for ntimes. interp2(Z) is the same as interp2(Z,1).

ZI = interp2(X,Y,Z,XI,YI,method) specifies an alternative interpolation method:

'nearest'	Nearest neighbor interpolation
'linear'	Bilinear interpolation (default)
'spline'	Cubic spline interpolation
'cubic'	Bicubuc interpolation

All interpolation methods require that X and Y be monotonic, and have the same format ("plaid") as if they were produced by meshgrid. If you provide two monotonic vectors, interp2 changes them to a plaid internally. Variable spacing is handled by mapping the given values in X, Y, XI, and YI to an equally spaced domain before interpolating. For faster interpolation when X and Y are equally spaced and monotonic, use the methods '*linear', '*cubic', '*spline', or '*nearest'.

ZI = interp2(...,method, extrapval) specifies a method and a scalar value for ZI outside of the domain created by X and Y. Thus, ZI equals extrapval for any value of YI or XI that is not spanned by Y or X respectively. A method must be specified to use extrapval. The default method is 'linear'.

Remarks

The interp2 command interpolates between data points. It finds values of a two-dimensional function 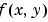underlying the data at intermediate points.

Interpolation is the same operation as table lookup. Described in table lookup terms, the table is tab = [NaN,Y; X,Z] and interp2 looks up the elements of XI in X, YI in Y, and, based upon their location, returns values ZI interpolated within the elements of Z.

Examples

Example 1. Interpolate the peaks function over a finer grid.

• [X,Y] = meshgrid(-3:.25:3);
  Z = peaks(X,Y);
  [XI,YI] = meshgrid(-3:.125:3);
  ZI = interp2(X,Y,Z,XI,YI);
  mesh(X,Y,Z), hold, mesh(XI,YI,ZI+15)
  hold off
  axis([-3 3 -3 3 -5 20])
  
  
  

Example 2. Given this set of employee data,

• years = 1950:10:1990;
  service = 10:10:30;
  wage = [150.697 199.592 187.625
            179.323 195.072 250.287
            203.212 179.092 322.767
            226.505 153.706 426.730
            249.633 120.281 598.243];
  

it is possible to interpolate to find the wage earned in 1975 by an employee with 15 years' service:

• w = interp2(service,years,wage,15,1975)
  w =
    190.6287
  

See Also

griddata, interp1, interp3, interpn, meshgrid

interp1

interp3

© 1994-2005 The MathWorks, Inc.