surf, surfc (MATLAB Functions)

3-D shaded surface plot

Syntax

surf(Z)
surf(X,Y,Z)
surf(X,Y,Z,C)
surf(...,'PropertyName',PropertyValue)
surf(axes_handle,...)
surfc(...)
h = surf(...)
h = surfc(...)
hsurface = surf('v6',...), hsurface = surfc('v6',...)

Description

Use surf and surfc to view mathematical functions over a rectangular region. surf and surfc create colored parametric surfaces specified by X, Y, and Z, with color specified by Z or C.

surf(Z) creates a a three-dimensional shaded surface from the z components in matrix Z, using x = 1:n and y = 1:m, where [m,n] = size(Z). The height, Z, is a single-valued function defined over a geometrically rectangular grid. Z specifies the color data as well as surface height, so color is proportional to surface height.

surf(X,Y,Z) creates a shaded surface using Z for the color data as well as surface height. X and Y are vectors or matrices defining the x and y components of a surface. If X and Y are vectors, length(X) = n and length(Y) = m, where [m,n] = size(Z). In this case, the vertices of the surface faces are 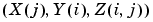triples.

surf(X,Y,Z,C) creates a shaded surface, with color defined by C. MATLAB performs a linear transformation on this data to obtain colors from the current colormap.

surf(...,'PropertyName',PropertyValue) specifies surface properties along with the data.

surf(axes_handles,...) and surfc(axes_handles,...) plots into the axes with handle axes_handle instead of the current axes (gca).

surfc(...) draws a contour plot beneath the surface.

h = surf(...) and h = surfc(...) return a handle to a surfaceplot graphics object.

Backward Compatible Version

hsurface = surf('v6',...) and hsurface = surfc('v6',...) returns the handles of surface objects instead of surfaceplot objects for compatibility with MATLAB 6.5 and earlier.

Algorithm

Abstractly, a parametric surface is parametrized by two independent variables, i and j, which vary continuously over a rectangle; for example, 1 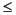i 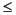m and 1 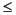j 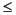n. The three functions x(i,j), y(i,j), and z(i,j) specify the surface. When i and j are integer values, they define a rectangular grid with integer grid points. The functions x(i,j), y(i,j), and z(i,j) become three m-by-n matrices, X, Y, and Z. Surface color is a fourth function, c(i,j), denoted by matrix C.

Each point in the rectangular grid can be thought of as connected to its four nearest neighbors.

       i-1,j
         |
i,j-1 - i,j - i,j+1
         |
       i+1,j

This underlying rectangular grid induces four-sided patches on the surface. To express this another way, [X(:) Y(:) Z(:)] returns a list of triples specifying points in 3-space. Each interior point is connected to the four neighbors inherited from the matrix indexing. Points on the edge of the surface have three neighbors; the four points at the corners of the grid have only two neighbors. This defines a mesh of quadrilaterals or a quad-mesh.

Surface color can be specified in two different ways: at the vertices or at the centers of each patch. In this general setting, the surface need not be a single-valued function of x and y. Moreover, the four-sided surface patches need not be planar. For example, you can have surfaces defined in polar, cylindrical, and spherical coordinate systems.

The shading function sets the shading. If the shading is interp, C must be the same size as X, Y, and Z; it specifies the colors at the vertices. The color within a surface patch is a bilinear function of the local coordinates. If the shading is faceted (the default) or flat, C(i,j) specifies the constant color in the surface patch:

 (i,j)   -   (i,j+1)
   |   C(i,j)  |
(i+1,j)  -  (i+1,j+1)

In this case, C can be the same size as X, Y, and Z and its last row and column are ignored. Alternatively, its row and column dimensions can be one less than those of X, Y, and Z.

The surf and surfc functions specify the viewpoint using view(3).

The range of X, Y, and Z or the current setting of the axes XLimMode, YLimMode, and ZLimMode properties (also set by the axis function) determines the axis labels.

The range of C or the current setting of the axes CLim and ClimMode properties (also set by the caxis function) determines the color scaling. The scaled color values are used as indices into the current colormap.

Examples

Display a surfaceplot and contour plot of the peaks surface.

[X,Y,Z] = peaks(30);
surfc(X,Y,Z)
colormap hsv
axis([-3 3 -3 3 -10 5])

Color a sphere with the pattern of +1s and -1s in a Hadamard matrix.

k = 5;
n = 2^k-1;
[x,y,z] = sphere(n);
c = hadamard(2^k);
surf(x,y,z,c);
colormap([1  1  0; 0  1  1])
axis equal

See Also

axis, caxis, colormap, contour, delaunay, mesh, pcolor, shading, trisurf, view

Properties for surfaceplot graphics objects

Creating Surfaces and Meshes for related functions

Representing a Matrix as a Surface for more examples

Coloring Mesh and Surface Plots for information about how to control the coloring of surfaces

support surf2patch