Inverse Radon Transform :: Transforms (Image Processing Toolbox User's Guide)

Image Processing Toolbox User's Guide

Inverse Radon Transform

The iradon function performs the inverse Radon transform, which is commonly used in tomography applications. This transform inverts the Radon transform (which was introduced in the previous section), and can therefore be used to reconstruct images from projection data.

As described in "Radon Transform" on page 8-21, given an image I and a set of angles theta, the radon function can be used to calculate the Radon transform.

```
R = radon(I,theta);
```

The function iradon can then be called to reconstruct the image I.

```
IR = iradon(R,theta);
```

In the example above, projections are calculated from the original image I. In most application areas, there is no original image from which projections are formed. For example, in X-ray absorption tomography, projections are formed by measuring the attenuation of radiation that passes through a physical specimen at different angles. The original image can be thought of as a cross section through the specimen, in which intensity values represent the density of the specimen. Projections are collected using special purpose hardware, and then an internal image of the specimen is reconstructed by iradon. This allows for noninvasive imaging of the inside of a living body or another opaque object.

iradon reconstructs an image from parallel-beam projections. In parallel-beam geometry, each projection is formed by combining a set of line integrals through an image at a specific angle.

The following figure illustrates how parallel-beam geometry is applied in X-ray absorption tomography. Note that there is an equal number of n emitters and n sensors. Each sensor measures the radiation emitted from its corresponding emitter, and the attenuation in the radiation gives a measure of the integrated density, or mass, of the object. This corresponds to the line integral that is calculated in the Radon transform.

The parallel-beam geometry used in the figure is the same as the geometry that was described in Radon Transform. f(x,y) denotes the brightness of the image and 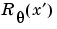is the projection at angle theta.

Parallel-Beam Projections Through an Object

Another geometry that is commonly used is fan-beam geometry, in which there is one source and n sensors. For more information, see Fan-Beam Projection Data. To convert parallel-beam projection data into fan-beam projection data, use the para2fan function.

Improving the Results

iradon uses the filtered backprojection algorithm to compute the inverse Radon transform. This algorithm forms an approximation of the image I based on the projections in the columns of R. A more accurate result can be obtained by using more projections in the reconstruction. As the number of projections (the length of theta) increases, the reconstructed image IR more accurately approximates the original image I. The vector theta must contain monotonically increasing angular values with a constant incremental angle 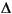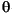capital delta theta . When the scalar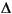 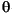theta is known, it can be passed to iradon instead of the array of theta values. Here is an example.

```
IR = iradon(R,Dtheta);
```

The filtered backprojection algorithm filters the projections in R and then reconstructs the image using the filtered projections. In some cases, noise can be present in the projections. To remove high frequency noise, apply a window to the filter to attenuate the noise. Many such windowed filters are available in iradon. The example call to iradon below applies a Hamming window to the filter. See the iradon reference page for more information.

```
IR = iradon(R,theta,'Hamming');
```

iradon also enables you to specify a normalized frequency, D, above which the filter has zero response. D must be a scalar in the range [0,1]. With this option, the frequency axis is rescaled so that the whole filter is compressed to fit into the frequency range [0,D]. This can be useful in cases where the projections contain little high-frequency information but there is high-frequency noise. In this case, the noise can be completely suppressed without compromising the reconstruction. The following call to iradon sets a normalized frequency value of 0.85.

```
IR = iradon(R,theta,0.85);
```

Using the Radon Transform to Detect Lines Example: Reconstructing an Image from Parallel Projection Data