| Image Processing Toolbox User's Guide | |
Radon Transform
The radon function in the Image Processing Toolbox computes projections of an image matrix along specified directions. A projection of a two-dimensional function f(x,y) is a set of line integrals. The radon function computes the line integrals from multiple sources along parallel paths, or beams, in a certain direction. The beams are spaced 1 pixel unit apart. To represent an image, the radon function takes multiple, parallel-beam projections of the image from different angles by rotating the source around the center of the image. The following figure shows a single projection at a specified rotation angle.
Parallel-Beam Projection at Rotation Angle Theta
Note
For information about creating projection data from line integrals along paths that radiate from a single source, called fan-beam projections, see Fan-Beam Projection Data. To convert parallel-beam projection data to fan-beam projection data, use the para2fan function.
|
For example, the line integral of f(x,y) in the vertical direction is the projection of f(x,y) onto the x-axis; the line integral in the horizontal direction is the projection of f(x,y) onto the y-axis. The following figure shows horizontal and vertical projections for a simple two-dimensional function.
Horizontal and Vertical Projections of a Simple Function
Projections can be computed along any angle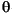 
. In general, the Radon transform of f(x,y) is the line integral of f parallel to the y´-axis
The following figure illustrates the geometry of the Radon transform.
Geometry of the Radon Transform
| | DCT and Image Compression | Plotting the Radon Transform | |
© 1994-2005 The MathWorks, Inc.
