ellip (Signal Processing Toolbox)

Elliptic (Cauer) filter design

Syntax

[b,a] = ellip(n,Rp,Rs,Wn)
[b,a] = ellip(n,Rp,Rs,Wn,'ftype')
[b,a] = ellip(n,Rp,Rs,Wn,'s')
[b,a] = ellip(n,Rp,Rs,Wn,'ftype','s')
[z,p,k] = ellip(...)
[A,B,C,D] = ellip(...)

Description

ellip designs lowpass, bandpass, highpass, and bandstop digital and analog elliptic filters. Elliptic filters offer steeper rolloff characteristics than Butterworth or Chebyshev filters, but are equiripple in both the pass- and stopbands. In general, elliptic filters meet given performance specifications with the lowest order of any filter type.

Digital Domain

[b,a] = ellip(n,Rp,Rs,Wn) designs an order n lowpass digital elliptic filter with normalized passband edge frequency Wn, Rp dB of ripple in the passband, and a stopband Rs dB down from the peak value in the passband. It returns the filter coefficients in the length n+1 row vectors b and a, with coefficients in descending powers of z.

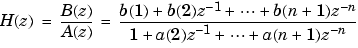
The normalized passband edge frequency is the edge of the passband, at which the magnitude response of the filter is -Rp dB. For ellip, the normalized cutoff frequency Wn is a number between 0 and 1, where 1 corresponds to half the sampling frequency (Nyquist frequency). Smaller values of passband ripple Rp and larger values of stopband attenuation Rs both lead to wider transition widths (shallower rolloff characteristics).

If Wn is a two-element vector, Wn = [w1 w2], ellip returns an order 2*n bandpass filter with passband w1 < 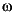< w2.

[b,a] = ellip(n,Rp,Rs,Wn,'ftype') designs a highpass, lowpass, or bandstop filter, where the string 'ftype' is one of the following.

'high' for a highpass digital filter with normalized passband edge frequency Wn
'low' for a lowpass digital filter with normalized passband edge frequency Wn
'stop' for an order 2*n bandstop digital filter if Wn is a two-element vector, Wn = [w1 w2]. The stopband is w1 < 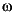< w2.

With different numbers of output arguments, ellip directly obtains other realizations of the filter. To obtain zero-pole-gain form, use three output arguments as shown below.

[z,p,k] = ellip(n,Rp,Rs,Wn) or

[z,p,k] = ellip(n,Rp,Rs,Wn,'ftype') returns the zeros and poles in length n column vectors z and p and the gain in the scalar k.

To obtain state-space form, use four output arguments as shown below:

[A,B,C,D] = ellip(n,Rp,Rs,Wn) or

[A,B,C,D] = ellip(n,Rp,Rs,Wn,'ftype') where A, B, C, and D are

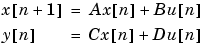
and u is the input, x is the state vector, and y is the output.

Analog Domain

[b,a] = ellip(n,Rp,Rs,Wn,'s') designs an order n lowpass analog elliptic filter with angular passband edge frequency Wn and returns the filter coefficients in the length n+1 row vectors b and a, in descending powers of s, derived from this transfer function:

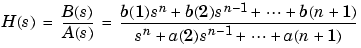
The angular passband edge frequency is the edge of the passband, at which the magnitude response of the filter is -Rp dB. For ellip, the angular passband edge frequency Wn must be greater than 0 rad/s.

If Wn is a two-element vector with w1 < w2, then ellip(n,Rp,Rs,Wn,'s') returns an order 2*n bandpass analog filter with passband w1 < < w2.

[b,a] = ellip(n,Rp,Rs,Wn,'ftype','s') designs a highpass, lowpass, or bandstop filter.

With different numbers of output arguments, ellip directly obtains other realizations of the analog filter. To obtain zero-pole-gain form, use three output arguments as shown below:

[z,p,k] = ellip(n,Rp,Rs,Wn,'s') or

[z,p,k] = ellip(n,Rp,Rs,Wn,'ftype','s') returns the zeros and poles in length n or 2*n column vectors z and p and the gain in the scalar k.

To obtain state-space form, use four output arguments as shown below:

[A,B,C,D] = ellip(n,Rp,Rs,Wn,'s') or

[A,B,C,D] = ellip(n,Rp,Rs,Wn,'ftype','s') where A, B, C, and D are

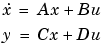
and u is the input, x is the state vector, and y is the output.

Examples

Example 1

For data sampled at 1000 Hz, design a sixth-order lowpass elliptic filter with a passband edge frequency of 300 Hz, which corresponds to a normalized value of 0.6, 3 dB of ripple in the passband, and 50 dB of attenuation in the stopband:

```
[b,a] = ellip(6,3,50,300/500);
```

The filter's frequency response is

freqz(b,a,512,1000)
title('n=6 Lowpass Elliptic Filter')

Example 2

Design a 20th-order bandpass elliptic filter with a passband from 100 to 200 Hz and plot its impulse response:

n = 10; Rp = 0.5; Rs = 20;
Wn = [100 200]/500;
[b,a] = ellip(n,Rp,Rs,Wn);
[y,t] = impz(b,a,101); stem(t,y)
title('Impulse Response of n=10 Elliptic Filter')

Limitations

For high order filters, the state-space form is the most numerically accurate, followed by the zero-pole-gain form. The transfer function form is the least accurate; numerical problems can arise for filter orders as low as 15.

Algorithm

The design of elliptic filters is the most difficult and computationally intensive of the Butterworth, Chebyshev Type I and II, and elliptic designs. ellip uses a five-step algorithm:

It finds the lowpass analog prototype poles, zeros, and gain using the ellipap function.
It converts the poles, zeros, and gain into state-space form.
It transforms the lowpass filter to a bandpass, highpass, or bandstop filter with the desired cutoff frequencies using a state-space transformation.
For digital filter design, ellip uses bilinear to convert the analog filter into a digital filter through a bilinear transformation with frequency prewarping. Careful frequency adjustment guarantees that the analog filters and the digital filters will have the same frequency response magnitude at Wn or w1 and w2.
It converts the state-space filter back to transfer function or zero-pole-gain form, as required.

See Also

besself, butter, cheby1, cheby2, ellipap, ellipord

dspopts ellipap